
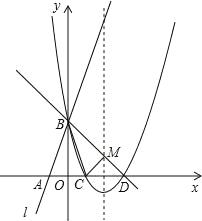
【题目】如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
(1)求直线BD和抛物线的解析式.
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.
【答案】(1)直线BD的解析式为:y=﹣x+3,抛物线的解析式为:y=(x﹣1)(x﹣3)=x2﹣4x+3;
(2)满足条件的点N坐标为:(0,0),(﹣3,0)或(0,﹣3);
(3)存在,点P的坐标为(4,3)或(﹣1,8).
【解析】
试题分析:(1)由待定系数法求出直线BD和抛物线的解析式;
(2)首先确定△MCD为等腰直角三角形,因为△BND与△MCD相似,所以△BND也是等腰直角三角形.如答图1所示,符合条件的点N有3个;
(3)如答图2、答图3所示,解题关键是求出△PBD面积的表达式,然后根据S△PBD=6的已知条件,列出一元二次方程求解.
试题解析:(1)∵直线l:y=3x+3与x轴交于点A,与y轴交于点B,
∴A(﹣1,0),B(0,3);
∵把△AOB沿y轴翻折,点A落到点C,∴C(1,0).
设直线BD的解析式为:y=kx+b,
∵点B(0,3),D(3,0)在直线BD上,
∴![]() ,
,
解得k=﹣1,b=3,
∴直线BD的解析式为:y=﹣x+3.
设抛物线的解析式为:y=a(x﹣1)(x﹣3),
∵点B(0,3)在抛物线上,
∴3=a×(﹣1)×(﹣3),
解得:a=1,
∴抛物线的解析式为:y=(x﹣1)(x﹣3)=x2﹣4x+3.
(2)抛物线的解析式为:y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线的对称轴为直线x=2,顶点坐标为(2,﹣1).
直线BD:y=﹣x+3与抛物线的对称轴交于点M,令x=2,得y=1,
∴M(2,1).
设对称轴与x轴交点为点F,则CF=FD=MF=1,
∴△MCD为等腰直角三角形.
∵以点N、B、D为顶点的三角形与△MCD相似,
∴△BND为等腰直角三角形.
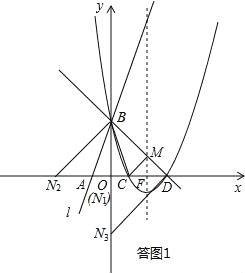
如答图1所示:
(I)若BD为斜边,则易知此时直角顶点为原点O,
∴N1(0,0);
(II)若BD为直角边,B为直角顶点,则点N在x轴负半轴上,
∵OB=OD=ON2=3,
∴N2(﹣3,0);
(III)若BD为直角边,D为直角顶点,则点N在y轴负半轴上,
∵OB=OD=ON3=3,
∴N3(0,﹣3).
∴满足条件的点N坐标为:(0,0),(﹣3,0)或(0,﹣3).
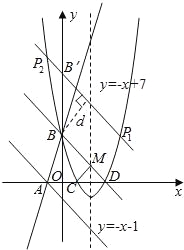
(3)方法一:
假设存在点P,使S△PBD=6,设点P坐标为(m,n).
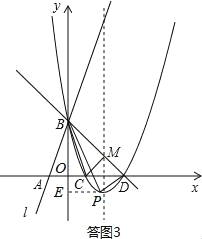
(I)当点P位于直线BD上方时,如答图2所示:
过点P作PE⊥x轴于点E,则PE=n,DE=m﹣3.
S△PBD=S梯形PEOB﹣S△BOD﹣S△PDE=![]() (3+n)m﹣
(3+n)m﹣![]() ×3×3﹣
×3×3﹣![]() (m﹣3)n=6,
(m﹣3)n=6,
化简得:m+n=7 ①,
∵P(m,n)在抛物线上,
∴n=m2﹣4m+3,
代入①式整理得:m2﹣3m﹣4=0,
解得:m1=4,m2=﹣1,
∴n1=3,n2=8,
∴P1(4,3),P2(﹣1,8);
(II)当点P位于直线BD下方时,如答图3所示:
过点P作PE⊥y轴于点E,则PE=m,OE=﹣n,BE=3﹣n.
S△PBD=S梯形PEOD+S△BOD﹣S△PBE=![]() (3+m)(﹣n)+
(3+m)(﹣n)+![]() ×3×3﹣
×3×3﹣![]() (3﹣n)m=6,
(3﹣n)m=6,
化简得:m+n=﹣1 ②,
∵P(m,n)在抛物线上,
∴n=m2﹣4m+3,
代入②式整理得:m2﹣3m+4=0,△=﹣7<0,此方程无解.
故此时点P不存在.
综上所述,在抛物线上存在点P,使S△PBD=6,点P的坐标为(4,3)或(﹣1,8).
方法二:
假设存在点P,使S△PBD=6,
过点P作直线l平行BD,则l与BD的距离为d,
∵BD=![]() =3
=3![]() ,
,
∴S△PBD=![]() BD×d,
BD×d,
∴d=2![]() ,
,
∵BD与y轴夹角为45°,
∴BB′=4,
∴将BD上移或下移4个单位,
①上移4个单位,l解析式为:y=﹣x+7,
∵y=x2﹣4x+3,
∴x2﹣3x﹣4=0,
∴x1=4,x2=﹣1,
②下移4个单位,l解析式为y=﹣x﹣1,
∵y=x2﹣4x+3,
∴x2﹣3x+4=0,△<0,∴此方程无解,
综上所述,点P的坐标为(4,3)或(﹣1,8).



科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中错误的是( )
A. 矩形的两条对角线相等 B. 等腰梯形的两条对角线互相垂直
C. 平行四边形的两条对角线互相平分 D. 正方形的两条对角线互相垂直且相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】居民区内的“广场舞”引起媒体关注,小王想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A.非常赞同;B.赞同但要有时间限制;C.无所谓;D.不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.
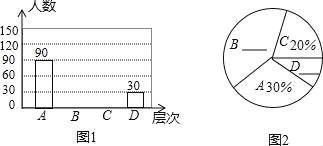
请你根据图中提供的信息解答下列问题:
(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列不等式变形正确的是( )
A.若a>b,则a﹣2>b﹣2
B.若-![]() ?a<2,则a<﹣4
?a<2,则a<﹣4
C.若a>b,则1﹣2a>1﹣2b
D.若a<b,则ac2<bc2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家.妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程S(km)与北京时间t(时)的函数图象如图所示.根据图象得到小亮结论,其中错误的是( )
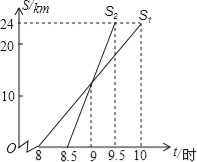
A. 小亮骑自行车的平均速度是12km/h
B. 妈妈比小亮提前0.5小时到达姥姥家
C. 妈妈在距家12km处追上小亮
D. 9:30妈妈追上小亮
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com