
【题目】如图,O是平面直角坐标系的原点.在四边形OABC中,AB∥OC,BC⊥x轴于C,A(1,1),B(3,1),动点P从O点出发,沿x轴正方向以2个单位/秒的速度运动.设P点运动的时间为t秒(0<t<2).
(1)求经过O、A、B三点的抛物线的解析式;
(2)过P作PD⊥OA于D,以点P为圆心,PD为半径作⊙P,⊙P在点P的右侧与x轴交于点Q.
①则P点的坐标为_____,Q点的坐标为_____;(用含t的代数式表示)
②试求t为何值时,⊙P与四边形OABC的两边同时相切;
③设△OPD与四边形OABC重叠的面积为S,请直接写出S与t的函数解析式.

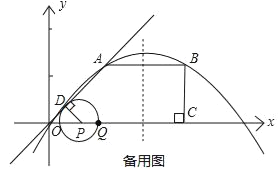
【答案】 (2t,0) ((2+![]() )t,0)
)t,0)
【解析】分析:(1)利用待定系数法即可得出结论;
(2)①先用含t的代数式表示出OP,再利用锐角三角函数表示出PD,进而表示出OQ即可得出结论;
②分⊙P与AB相切时,⊙P与BC相切时两种情况,利用直线和圆相切的性质建立方程求解即可;
③分0<t≤1,1<t≤![]() ,
,![]() <t<2三种情况,利用几何图形的面积公式即可得出结论.
<t<2三种情况,利用几何图形的面积公式即可得出结论.
详解:(1)因为抛物线经过原点O,所以设抛物线解析式为y=ax2+bx.
又因为抛物线经过A(1,1),B(3,1),
所以有![]() 解得
解得![]() ,
,
所以抛物线解析式为y=﹣![]() x2+
x2+![]() x
x
(2)①由运动知,OP=2t,
∴P(2t,0),
∵A(1,1),
∴∠AOC=45°,
∵PD⊥OA,
∴PD=OPsin∠AOC=![]() t,
t,
∵PD为半径作⊙P,⊙P在点P的右侧与x轴交于点Q,
∴PQ=PD=![]() t,
t,
∴OQ=OP+PQ=2t+![]() t=(2+
t=(2+![]() )t
)t
∴Q((2+![]() )t,0),
)t,0),
故答案为(2t,0),((2+![]() )t,0);
)t,0);
②当⊙P与AB相切时,![]() t=1,所以t=
t=1,所以t=![]() ;
;
当⊙P与BC相切时,即点Q与点C重合,所以(2+![]() )t=3,解得t=
)t=3,解得t=![]() .
.
(3)①当0<t≤1,如图1,重叠部分的面积是S△OPQ,
过点A作AF⊥x轴于点F,
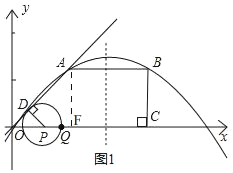
∵A(1,1),
在Rt△OAF中,AF=OF=1,∠AOF=45°,
在Rt△OPQ中,
∴PQ=OQ=2tcos45°=![]() t,
t,
∴S=![]() (
(![]() t)2=t2,
t)2=t2,
②当1<t≤![]() ,如图2,设PQ交AB于点G,
,如图2,设PQ交AB于点G,
作GH⊥x轴于点H,∠OPQ=∠QOP=45°,
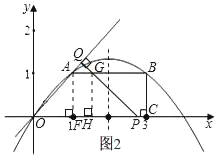
则四边形OAGP是等腰梯形,PH=GH=AF=1,
重叠部分的面积是S梯形OAGP.
∴AG=FH=OP﹣PH﹣OF=2t﹣2,
∴S=(AG+OP)AF=![]() (2t+2t﹣2)×1=2t﹣1.
(2t+2t﹣2)×1=2t﹣1.
③当![]() <t<2,如图3,设PQ与AB交于点M,交BC于点N,
<t<2,如图3,设PQ与AB交于点M,交BC于点N,
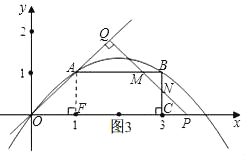
重叠部分的面积是S五边形OAMNC.
因为△PNC和△BMN都是等腰直角三角形,
所以重叠部分的面积是S五边形OAMNC=S梯形OABC﹣S△BMN.
∵B(3,1),OP=2t,
∴CN=PC=OP﹣OC=2t﹣3,
∴BM=BN=1﹣(2t﹣3)=4﹣2t,
∴S=![]() (2+3)×1﹣
(2+3)×1﹣![]() (4﹣2t)2=﹣2t2+8t﹣
(4﹣2t)2=﹣2t2+8t﹣![]() .
.
即:S=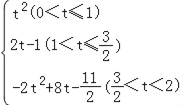 .
.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,直线y=x+1与双曲线![]() 的一个交点为P(m,6).
的一个交点为P(m,6).
(1)求k的值;
(2)M(2,a),N(n,b)分别是该双曲线上的两点,直接写出当a>b时,n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:解分式不等式![]() <0
<0
解:根据实数的除法法则:同号两数相除得正数,异号两数相除得负数,因此,原不等式可转化为:
①![]() 或②
或②![]()
解①得:无解,解②得:﹣2<x<1
所以原不等式的解集是﹣2<x<1
请仿照上述方法解下列分式不等式:(1)![]() >0;(2)
>0;(2)![]() <0.
<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
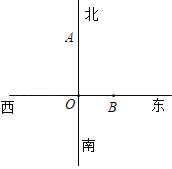
【题目】如图,一艘货轮位于O地,发现灯塔A在它的正北方向上,这艘货轮沿正东方向航行50千米,到达B地,此时用雷达测得灯塔A与货轮的距离为100千米.
(1)在图中作出灯塔A的位置,并作射线BA;
(2)以正北,正南方向为基准,借助量角器,描述灯塔A在B地的什么方向上(精确到1°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平面上![]() 四个点.
四个点.
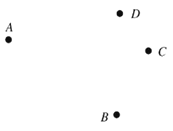
(1)按下列要求画图(不写画法)
①连接![]() ,
,![]() ;②作直线
;②作直线![]() ;③作射线
;③作射线![]() ,交
,交![]() 于点
于点![]() .
.
(2)在(1)所画的图形中共有__________条线段,__________条射线. (所画图形中不能再添加标注其他字母);
(3)通过测量线段![]() ,
,![]() ,
,![]() ,可知
,可知![]() __________
__________![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”),可以解释这一现象的基本事实为:_______________________.
”),可以解释这一现象的基本事实为:_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形![]() 的边长是1米;
的边长是1米;
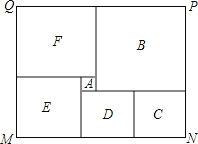
(1)若设图中最大正方形![]() 的边长是
的边长是![]() 米,请用含
米,请用含![]() 的代数式分别表示出正方形
的代数式分别表示出正方形![]() 的边长
的边长
(2)观察图形的特点可知,长方形相对的两边是相等的(即![]() ,
, ![]() )请根据以上结论,求出
)请根据以上结论,求出![]() 的值
的值
(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙工程队单独铺设分别需要10天、15天完成,如果两队从同一位置开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,还要多少天完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛.各参赛选手成绩的数据分析如下表所示,则以下判断错误的是( )
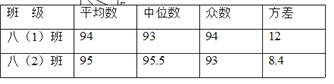
A. 八(2)班的总分高于八(1)班 B. 八(2)班的成绩比八(1)班稳定
C. 八(2)班的成绩集中在中上游 D. 两个班的最高分在八(2)班
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com