
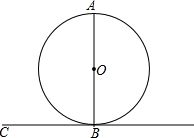
 如图,AB是圆O的直径,直线BC与圆O相切于点B.
如图,AB是圆O的直径,直线BC与圆O相切于点B. 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
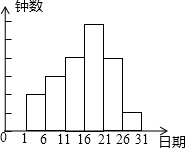 在学校开展的综合实践活动中,九(1)班进行了小制作评比,作品上交时间为5月1日到30日,评委会把同学们上交作品的件数按5天一组统计,绘制了频数分布直方图,如图所示,已知从左至右各小长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列问题:
在学校开展的综合实践活动中,九(1)班进行了小制作评比,作品上交时间为5月1日到30日,评委会把同学们上交作品的件数按5天一组统计,绘制了频数分布直方图,如图所示,已知从左至右各小长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE.
如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE.查看答案和解析>>
科目:初中数学 来源: 题型:
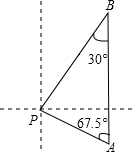 马航MH370 客机“失联”,我国“海巡01号”前往搜寻.如图某天上午9时,“海巡01号”轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(精确到0.1)
马航MH370 客机“失联”,我国“海巡01号”前往搜寻.如图某天上午9时,“海巡01号”轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(精确到0.1)查看答案和解析>>
科目:初中数学 来源: 题型:
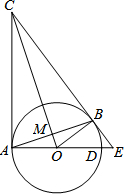 如图,CA、CB为⊙O的切线,切点分别为A、B.直径延长AD与CB的延长线交于点E. AB、CO交于点M,连接OB.
如图,CA、CB为⊙O的切线,切点分别为A、B.直径延长AD与CB的延长线交于点E. AB、CO交于点M,连接OB.| 1 |
| 2 |
| ||
| 10 |
| BE |
| AE |
查看答案和解析>>
科目:初中数学 来源: 题型:
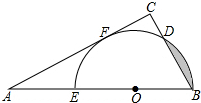 如图,把一块三角板(∠A=30°,∠C=90°,AC=6
如图,把一块三角板(∠A=30°,∠C=90°,AC=6| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
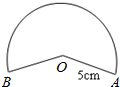 小明用图中的扇形纸片作一个圆锥的侧面,已知扇形的半径为5cm,面积是15πcm2,那么这个的圆锥底面半径是( )
小明用图中的扇形纸片作一个圆锥的侧面,已知扇形的半径为5cm,面积是15πcm2,那么这个的圆锥底面半径是( )| A、2cm | B、3cm |
| C、4cm | D、5cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com