
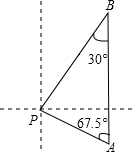
 马航MH370 客机“失联”,我国“海巡01号”前往搜寻.如图某天上午9时,“海巡01号”轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(精确到0.1)
马航MH370 客机“失联”,我国“海巡01号”前往搜寻.如图某天上午9时,“海巡01号”轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(精确到0.1)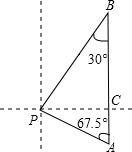 解:过点P作PC⊥AB,垂足为C,设PC=x海里.
解:过点P作PC⊥AB,垂足为C,设PC=x海里.| PC |
| AC |
| PC |
| tan67.5° |
| 5x |
| 12 |
| PC |
| BC |
| x |
| tan30° |
| 3 |
| 5x |
| 12 |
| 3 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
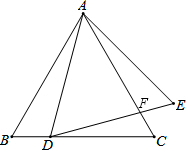 如图,点D在等边△ABC的BC边上,△ADE为等边三角形,DE与AC交于点F.
如图,点D在等边△ABC的BC边上,△ADE为等边三角形,DE与AC交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
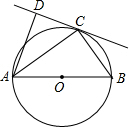 已知:AB为⊙O的直径,C为⊙O上一点,CD是⊙O的切线,AD⊥CD于D.
已知:AB为⊙O的直径,C为⊙O上一点,CD是⊙O的切线,AD⊥CD于D.查看答案和解析>>
科目:初中数学 来源: 题型:
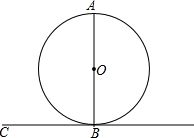 如图,AB是圆O的直径,直线BC与圆O相切于点B.
如图,AB是圆O的直径,直线BC与圆O相切于点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com