
【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.

(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
【答案】见解析
【解析】(1)证明:∵∠A=∠ABC=90°,
∴BC∥AD,
∴∠CBE=∠DFE,
在△BEC与△FED中,
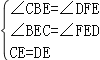 ,
,
∴△BEC≌△FED,
∴BE=FE,
又∵E是边CD的中点,
∴CE=DE,
∴四边形BDFC是平行四边形;
(2)①BC=BD=3时,由勾股定理得,AB=![]() =
=![]() =2
=2![]() ,
,
所以,四边形BDFC的面积=3×2![]() =6
=6![]() ;
;
②BC=CD=3时,过点C作CG⊥AF于G,则四边形AGCB是矩形,
所以,AG=BC=3,
所以,DG=AG﹣AD=3﹣1=2,
由勾股定理得,CG=![]() =
=![]() =
=![]() ,
,
所以,四边形BDFC的面积=3×![]() =3
=3![]() ;
;
③BD=CD时,BC边上的中线应该与BC垂直,从而得到BC=2AD=2,矛盾,此时不成立;
综上所述,四边形BDFC的面积是6![]() 或3
或3![]() .
.


科目:初中数学 来源: 题型:
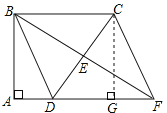
【题目】在△ABC中,AC=BC,∠ACB=90°,点D为AC的中点.
(1)如图1,E为线段DC上任意一点,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,过点F作FH⊥FC,交直线AB于点H.判断FH与FC的数量关系并加以证明;
(2)如图2,若E为线段DC的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】冬季某天我国三个城市的最高气温分别是-11℃,3℃,-3℃,它们任意两城市中最大的温差是( )
A. 6℃ B. 8℃ C. 13℃ D. 14℃
查看答案和解析>>
科目:初中数学 来源: 题型:
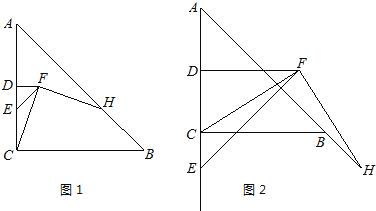
【题目】现有若干张如图1的正方形硬纸片A.B和长方形硬纸片C.
(1)小明利用这些硬纸片拼成了如图2的一个新正方形,用两种不同的方法,计算出了新正方形的面积,由此,他得到了一个等式:_____________
(2)小明再取其中的若干张(三种纸片都取到)拼成一个面积为a2+nab+2b2长方形,则n可取的正整数值为____,并请在图3位置画出拼成的图形。
(3)根据拼图的经验,请将多项式a2+4ab+3b2分解因式:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在X轴正半轴上,B在Y轴的负半轴,过点B画MN∥x轴;C是Y轴上一点,连接AC,作CD⊥CA.
(1)如图(1),请直接写出∠CA0与∠CDB的数量关系.
(2)如图(2),在题(1)的条件下,∠CAO的角平分线与∠CDB的角平分线相交于点P,求∠APD的度数.
(3)如图(2),在题(1)、(2)的条件下,∠CAX的角平分线与∠CDN的角平分线相交于点Q,请直接写出∠APD与∠AQD数量关系.
(4)如图(3),点C在Y轴的正半轴上运动时,∠CAO的角平分线所在的直线与∠CDB的角平分线相交于点P,∠APD的大小是否变化?若不变,直接写出其值;若变化,说明理由.
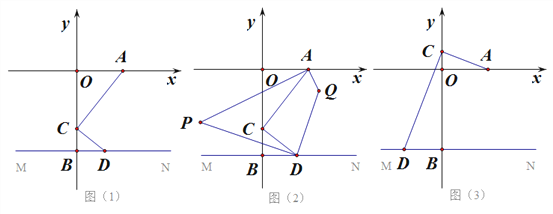
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2)
(1)写出点A、B的坐标:A( , )、B( , )
(2)将△ABC先向左平移1个单位长度,再向上平移2个单位长度,得到△A′B′C′,画出△A′B′C′
(3)写出三个顶点坐标A′( 、 )、B′( 、 )、C′ ( 、 )
(4)求△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com