
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论: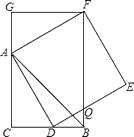
①AC=FG; ②S△FAB:S四边形CBFG=1:2;
③∠ABC=∠ABF; ④AD2=FQAC,
其中正确的结论的个数是( )
A.1
B.2
C.3
D.4
【答案】D
【解析】①∵四边形ADEF为正方形,
∴AD=AF,∠FAD=90°,
∴∠FAG+∠CAD=90°,
又∵FG⊥CA,
∴∠FGA=90°,
∴∠FAG+∠AFG=90°,
∴∠CAD=∠AFG,
在△AGF和△DCA中,
∵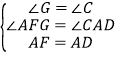 ,
,
∴△AGF≌△DCA(AAS),
∴FG=CA.
故①正确.
②∵BC=AC,FG=CA,
∴BC=FG,
又∵FG⊥CA,∠ACB=90°,
∴FG∥BC,
∴四边形BCGF是平行四边形,
又∵∠ACB=90°,
∴平行四边形BCGF是矩形,
∴∠CBF=90°,
∴S△FAB=![]() BFBC,
BFBC,
S四边形CBFG=BFBC,
∴S△FAB:S四边形CBFG=1:2;
故②正确.
③∵CA=CB,∠C=∠CBF=90°,
∴∠BAC=∠CBA=45°,
∴∠FBA=45°,
故③正确.
④∵∠ADE=∠CBF=90°,
∴∠ADC+∠BDQ=90°,
∠BQD+∠BDQ=90°,
∴∠ADC=∠BQD,
又∵∠FQE=∠BQD,
∴∠ADC=∠FQE,∠E=∠C=90°,
∴△ACD∽△FEQ,
∴AC:FE=AD:FQ,
又∵FE=AD,
∴AD2=FQAC,
故④正确.
所以答案是:D.
【考点精析】利用正方形的性质和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和25,则△EDF的面积为( )

A. 35B. 25C. 15D. 12.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠α和∠β互补,且∠α>∠β,下列表示角的式子:①90°-∠β;②∠α-90°;③![]() (∠α+∠β);④
(∠α+∠β);④![]() (∠α-∠β).其中能表示∠β的余角的有( )个.
(∠α-∠β).其中能表示∠β的余角的有( )个.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明将两块完全相同的直角三角形纸片的直角顶点C叠放在一起,若保持△BCD不动,将△ACE绕直角顶点C旋转.
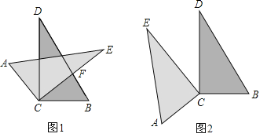
(1)如图1,如果CD平分∠ACE,那么CE是否平分∠BCD?答:______(填写“是”或“否”);
(2)如图1,若∠DCE=35,则∠ACB=______;若∠ACB=140,则∠DCE=______;
(3)当△ACE绕直角顶点C旋转到如图1的位置时,猜想∠ACB与∠DCE的数量关系,并说明理由;
(4)当△ACE绕直角顶点C旋转到如图2的位置时,上述关系是否依然成立,请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在一次测量旗杆高度的活动中,某小组使用的方案如下:AB表示某同学从眼睛到脚底的距离,CD表示一根标杆,EF表示旗杆,AB、CD、EF都垂直于地面。若AB=1.6m,CD=2m,人与标杆之间的距离BD=1m,标杆与旗杆之间的距离DF=30m,求旗杆EF的高度。
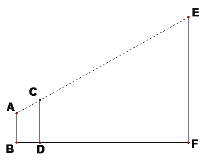
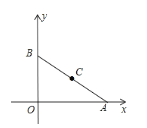
(2)如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6),点C是线段AB的中点。请问在x轴上是否存在一点P,使得以P、A、C为顶点的三角形与△AOB相似?若存在,求出P点坐标(写出计算的过程);若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据所学知识完成小题:
(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等边△ABE和等边△ACD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.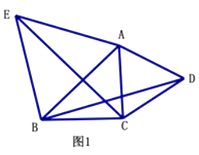
(2)【深入探究】如图2,△ABC中,∠ABC=45°,AB=5cm,BC=3cm,分别以AB、AC为边向外作正方形ABNE和正方形ACMD,连接BD,求BD的长.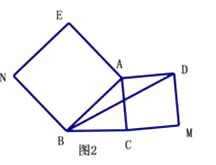
(3)如图3,在(2)的条件下,以AC为直角边在线段AC的左侧作等腰直角△ACD,求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com