
【题目】如图,小明将两块完全相同的直角三角形纸片的直角顶点C叠放在一起,若保持△BCD不动,将△ACE绕直角顶点C旋转.
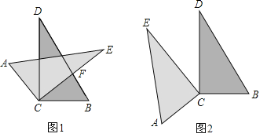
(1)如图1,如果CD平分∠ACE,那么CE是否平分∠BCD?答:______(填写“是”或“否”);
(2)如图1,若∠DCE=35,则∠ACB=______;若∠ACB=140,则∠DCE=______;
(3)当△ACE绕直角顶点C旋转到如图1的位置时,猜想∠ACB与∠DCE的数量关系,并说明理由;
(4)当△ACE绕直角顶点C旋转到如图2的位置时,上述关系是否依然成立,请说明理由;
【答案】(1)是;(2)145°,40°;(3)∠ACB+∠DCE=180°,理由见解析;(4)成立,理由见解析
【解析】
(1)CD平分∠ACE,那么可得∠DCE=45°,进而求得∠BCF是45°,那么CE平分∠BCD;
(2)由∠DCE=35°可先求出∠ACD=55°,再结合∠ACB=∠DCB+∠ACD,∠BCD=90°即可求解;由∠ACB=140°,可先求出∠ACD从而求出∠DCE.
(3)根据∠ACE=∠DCB=90°,以及∠ACB=∠ACE+∠BCE,即可得出∠ACB+∠DCE=180°.
(4)根据周角定义,再结合已知条件,可以得出∠ACB+∠DCE=180°.
解:(1)∵CD平分∠ACE,∠ACE=90°,
∴∠ACD=∠DCE=45°,
∵∠DCB=90°,
∴∠ECB=90°∠DCE=45°
∴∠DCE=∠ECB,
∴CE平分∠DCB,
故答案为:是.
(2)∵∠ACD+∠DCE=90°,∠DCE=35°,
∴∠ACD=55°,
∴∠ACB=∠DCB+∠ACD=90°+55°=145°;
当∠ACB=140°,
∴∠ACD=∠ACB∠DCB=50°,
∴∠DCE=∠ACE∠ACD=40°.
故答案分别为:145°,40°.
(3)结论:∠ACB+∠DCE=180°,
理由:∵∠ACE=∠DCB=90°,∠ACB=∠ACE+∠BCE,
∴∠ACB+∠DCE=∠ACE+∠BCE+∠DCE=∠ACE+∠DCB=90°+90°=180°,
(4)成立.
理由∵∠ACE+∠DCB=180°,
又∵∠ACB+∠DCE+∠ACE+∠DCB=360°,∠ACE=∠DCB=90°,
∴∠ACB+∠DCE=360°(∠ACE+∠DCB)=180°.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).

(1)在图中作出△ABC关于y轴对称的△A1B1C1;写出点△A1,B1,C1的坐标(直接写答案):A1 ;B1 ;C1 ;
(2)△A1B1C1的面积为 ;
(3)在y轴上画出点P,使PB+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB表示路灯,当身高为1.6米的小名站在离路灯1.6的D处时,他测得自己在路灯下的影长DE与身高CD相等,当小明继续沿直线BD往前走到E点时,画出此时小明的影子,并计算此时小明的影长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,O,B在同一条直线上,∠AOB=90°,∠AOE=∠DOB,则下列结论:①∠EOD=90°;②∠COE=∠AOD;③∠AOE+∠DOC=180![]() ;④互余的角有4对.其中正确的有( )
;④互余的角有4对.其中正确的有( )
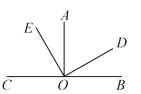
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论: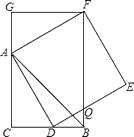
①AC=FG; ②S△FAB:S四边形CBFG=1:2;
③∠ABC=∠ABF; ④AD2=FQAC,
其中正确的结论的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC,∠C=90°,∠ABC=40°,按以下步骤作图:
①以点A为圆心,小于AC的长为半径.画弧,分别交AB、AC于点E、F;
②分别以点E、F为圆心,大于![]() EF的长为半径画弧,两弧相交于点G;
EF的长为半径画弧,两弧相交于点G;
③作射线AG,交BC边于点D,则∠ADC的度数为________.

【答案】65°
【解析】由题意可知,所作的射线AG是∠BAC的角平分线.
∵在△ABC中,∠C=90°,∠ABC=40°,
∴∠BAC=180°-90°-40°=50°,
∴∠CAD=![]() ∠BAC=25°,
∠BAC=25°,
∴∠ADC=180°-90°-25°=65°.
【题型】填空题
【结束】
13
【题目】如图所示,已知线段AB,∠α,∠β,分别过A、B作∠CAB=∠α,∠CBA=∠β.(不写作法,保留作图痕迹)


![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知四边形ABCD、ADEF都是菱形,∠BAD=∠FAD, ∠BAD为锐角.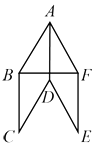
(1)求证:AD⊥BF;
(2)若BF=BC,求∠ADC的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
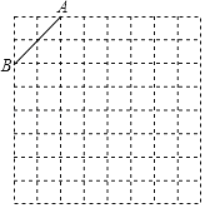
【题目】如图是规格为8×8的正方形网格,每个小方格都是边长为1的正方形.
(1)在网格中建立平面直角坐标系,使A点坐标为(﹣2,4);
(2)在第二象限内的格点(网格线的交点)上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是_____.
(3)画出△ABC关于y轴对称的△A′B′C′.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com