练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，点C，O，B在同一条直线上，∠AOB=90°，∠AOE=∠DOB，则下列结论：①∠EOD=90°；②∠COE=∠AOD；③∠AOE+∠DOC=180；④互余的角有4对．其中正确的有（ ）

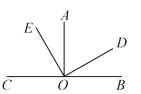
    A.1个B.2个C.3个D.4个

    【答案】D

    【解析】

    结合图形，根据平角的定义、余角的性质和等量代换可以进行判断，注意运用角的和差的运算．

    解：∵∠AOB＝90°
    ∴∠AOD＋∠BOD＝90°
    ∵∠AOE＝∠DOB
    ∴∠AOE＋∠AOD＝90°，即∠EOD＝90°，故①正确；

    ∵∠AOE+∠COE=90°，
    ∴∠COE＝∠AOD，故②正确，

    ∴∠COE＋∠BOD＝90°，

    ∴互余的角有∠AOD与∠BOD、∠AOE与∠AOD、∠AOE与∠COE、∠COE与∠BOD，共4对，故④正确；

    ∵∠DOC+∠BOD=180°，

    ∴∠AOE+∠DOC=180，故③正确；
    ∴①②③④都正确．
    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】问题：如图1，在四边形ABCD中，点P为AB上一点，∠DPC=∠A=∠B=90°．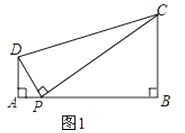

    （1）求证：ADBC=APBP．
    （2）探究：如图2，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=θ时，上述结论是否依然成立？说明理由．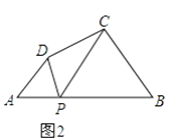

    （3）应用：请利用（1）（2）获得的经验解决问题：
    如图3，在△ABD中，AB=12，AD=BD=10．点P以每秒1个单位长度的速度，由点A出发，沿边AB向点B运动，且满足∠DPC=∠A．设点P的运动时间为t（秒），当以D为圆心，以DC为半径的圆与AB相切，求t的值．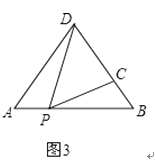

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：△ABC是等边三角形．

    （1）如图，点D在AB边上，点E在AC边上，BD＝CE，BE与CD交于点F．试判断BF与CF的数量关系，并加以证明；

    （2）点D是AB边上的一个动点，点E是AC边上的一个动点，且BD＝CE，BE与CD交于点F．若△BFD是等腰三角形，求∠FBD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】合肥市某学校搬迁,教师和学生的寝室数量在增加,若该校今年准备建造三类不同的寝室,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.

    (1)若2015年学校寝室数为64个,2017年建成后寝室数为121个,求2015至2017年的平均增长率;

    (2)若建成后的寝室可供600人住宿,求单人间的数量;

    (3)若该校今年建造三类不同的寝室的总数为180个,则该校的寝室建成后最多可供多少师生住宿?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知∠α和∠β互补，且∠α＞∠β，下列表示角的式子：①90°-∠β；②∠α-90°；③（∠α+∠β）；④（∠α-∠β）．其中能表示∠β的余角的有（ ）个．

    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某地区100个家庭收入按从高到低是5800，……，10000元各不相同，在输入计算时，把最大的数错误地输成100000元，则依据错误的数据算出的平均数比实际平均数多（ ）

    A. 900元B. 942元C. 90000元D. 9000元

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，小明将两块完全相同的直角三角形纸片的直角顶点C叠放在一起，若保持△BCD不动，将△ACE绕直角顶点C旋转．

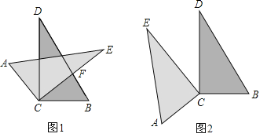
    （1）如图1，如果CD平分∠ACE，那么CE是否平分∠BCD?答：______（填写“是”或“否”）；

    （2）如图1，若∠DCE=35，则∠ACB=______；若∠ACB=140，则∠DCE=______；

    （3）当△ACE绕直角顶点C旋转到如图1的位置时，猜想∠ACB与∠DCE的数量关系，并说明理由；

    （4）当△ACE绕直角顶点C旋转到如图2的位置时，上述关系是否依然成立，请说明理由；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，直线，点为平面上一点，连接与．

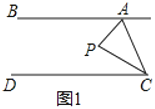
    （1）如图1，点在直线、之间，当，时，求．

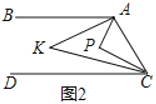
    （2）如图2，点在直线、之间左侧，与的角平分线相交于点，写出与之间的数量关系，并说明理由．

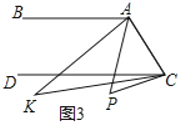
    （3）如图3，点落在下方，与的角平分线相交于点，与有何数量关系？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解：在以后你的学习中，我们会学习一个定理：直角三角形斜边上的中线等于斜边的一半，即：如图1，在Rt△ABC中，∠ACB＝90°，若点D是斜边AB的中点，则CD＝AB．

    灵活应用：如图2，△ABC中，∠BAC＝90°，AB＝6，AC＝8，点D是BC的中点，连接AD，将△ACD沿AD翻折得到△AED，连接BE，CE．

    （1）填空：AD＝　 　；

    （2）求证：∠BEC＝90°；

    （3）求BE．

    查看答案和解析>>

    同步练习册答案