
【题目】问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.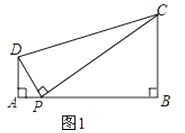
(1)求证:ADBC=APBP.
(2)探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.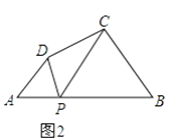
(3)应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=12,AD=BD=10.点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),当以D为圆心,以DC为半径的圆与AB相切,求t的值.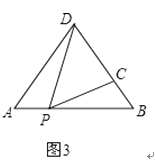
【答案】
(1)证明:如图1,
∵∠DPC=∠A=∠B=90°,
∴∠ADP+∠APD=90°,
∠BPC+∠APD=90°,
∴∠APD=∠BPC,
∴△ADP∽△BPC,
∴ ![]() ,
,
∴ADBC=APBP
(2)结论ADBC=APBP仍成立;
理由:证明:如图2,∵∠BPD=∠DPC+∠BPC,
又∵∠BPD=∠A+∠APD,
∴∠DPC+∠BPC=∠A+∠APD,
∵∠DPC=∠A=θ,
∴∠BPC=∠APD,
又∵∠A=∠B=θ,
∴△ADP∽△BPC,
∴ ![]() ,
,
∴ADBC=APBP;
(3)解:如下图,过点D作DE⊥AB于点E,
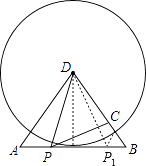
∵AD=BD=10,AB=12,
∴AE=BE=6
∴DE= ![]() =8,
=8,
∵以D为圆心,以DC为半径的圆与AB相切,
∴DC=DE=8,
∴BC=10﹣8=2,
∵AD=BD,
∴∠A=∠B,
又∵∠DPC=∠A,
∴∠DPC=∠A=∠B,
由(1)(2)的经验得ADBC=APBP,
又∵AP=t,BP=12﹣t,
∴t(12﹣t)=10×2,
∴t=2或t=10,
∴t的值为2秒或10秒
【解析】(1)要证ADBC=APBP,将等积式转化为比列式,可知需证△ADP∽△BPC,根据已知易证证明∠APD=∠BPC,即可得出结论。
(2)此题需证△ADP∽△BPC,还差一个条件,根据三角形外角性质得出∠BPD=∠DPC+∠BPC,∠BPD=∠A+∠APD,结合已知得出∠BPC=∠APD,即可证得结论。
(3)抓住已知AD=BD,过点D作DE⊥AB于点E,根据等腰三角形的性质及勾股定理求出DE的长,再以D为圆心,以DC为半径的圆与AB相切,得出DC=DE=8,从而求出BC的长,再证明∠DPC=∠A=∠B,根据前两题的证明过程可知ADBC=APBP,建立方程求出t的值。
【考点精析】根据题目的已知条件,利用因式分解法和三角形的外角的相关知识可以得到问题的答案,需要掌握已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.


科目:初中数学 来源: 题型:
【题目】如图,OP平分∠BOA,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论中错误的是( )

A. PC=PD B. OC=OD C. OC=OP D. ∠CPO=∠DPO
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现与探索
你能求 x 1x2019 x2018 x2017 x 1 的值吗?
遇到这样的问题,我们可以先思考一下,从简单的情形手.先分别计算下列各式的值:
① x 1 x 1 x2 1 ;
② x 1x2 x 1 x3 1 ;
③ x 1x3 x2 x 1 x4 1 ;
由此我们可以得到:
x 1x2019 x2018 x2017 x 1 ; 请你利用上面的结论,完成下面两题的计算:
(1)32019 32018 32017 3 1 ;
(2)250 249 248 2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 , 已知 ∠1+∠2=180,∠3=∠B, 试说明 DE ∥ BC. 下面是部分推导过程,请你在括号内填上推导依据或内容:

证明: ∵∠1+∠2=180( 已知 )
∠1=∠4( )
∴∠2+∠4=180( )
∵EH ∥ AB( )
∴∠B=∠EHC( )
∵∠3=∠B( )
∴∠3=∠EHC( 等量代换 )
∴DE ∥ BC( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,B(2,0),A(6,6),M(0,6),P点为y轴上一动点。
(1)当P点在线段OM上运动时,试问是否存在一个点P使![]() =13,若存在,请求出P点耳朵坐标;若不存在,请说明理由.
=13,若存在,请求出P点耳朵坐标;若不存在,请说明理由.
(2)当点P在y的正半轴上运动时(不包括O,M),∠PAM,∠APB,∠PBO三者之间是否存在某种数量关系,如果有,请利用所学的知识找出并证明;如果没有,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).

(1)在图中作出△ABC关于y轴对称的△A1B1C1;写出点△A1,B1,C1的坐标(直接写答案):A1 ;B1 ;C1 ;
(2)△A1B1C1的面积为 ;
(3)在y轴上画出点P,使PB+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
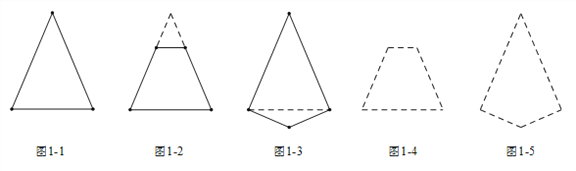
【题目】在我们认识的多边形中,有很多轴对称图形.有些多边形,边数不同对称轴的条数也不同;有些多边形,边数相同但却有不同数目的对称轴.回答下列问题:
(1)非等边的等腰三角形有________条对称轴,非正方形的长方形有________条对称轴,等边三角形有___________条对称轴;
(2)观察下列一组凸多边形(实线画出),它们的共同点是只有1条对称轴,其中图1-2和图1-3都可以看作由图1-1修改得到的,仿照类似的修改方式,请你在图1-4和图1-5中,分别修改图1-2和图1-3,得到一个只有1条对称轴的凸五边形,并用实线画出所得的凸五边形;
(3)小明希望构造出一个恰好有2条对称轴的凸六边形,于是他选择修改长方形,图2中是他没有完成的图形,请用实线帮他补完整个图形;
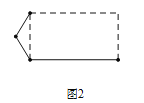
(4)请你画一个恰好有3条对称轴的凸六边形,并用虚线标出对称轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,O,B在同一条直线上,∠AOB=90°,∠AOE=∠DOB,则下列结论:①∠EOD=90°;②∠COE=∠AOD;③∠AOE+∠DOC=180![]() ;④互余的角有4对.其中正确的有( )
;④互余的角有4对.其中正确的有( )
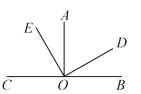
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com