
【题目】发现与探索
你能求 x 1x2019 x2018 x2017 x 1 的值吗?
遇到这样的问题,我们可以先思考一下,从简单的情形手.先分别计算下列各式的值:
① x 1 x 1 x2 1 ;
② x 1x2 x 1 x3 1 ;
③ x 1x3 x2 x 1 x4 1 ;
由此我们可以得到:
x 1x2019 x2018 x2017 x 1 ; 请你利用上面的结论,完成下面两题的计算:
(1)32019 32018 32017 3 1 ;
(2)250 249 248 2 .
【答案】![]() ;(1)
;(1) ![]() ; (2)
; (2) ![]() .
.
【解析】
根据平方差公式可得第1个式子的结果,利用多项式乘以多项式的方法可得出第2、3个式子的结果;从而总结出规律是(x-1)(x2019+x2018+x2017+…+x+1)=x2020-1;
(1)式子乘以![]() ,然后根据上上面发现的结论进行计算即可;
,然后根据上上面发现的结论进行计算即可;
(2)原式加1减1,除-1外其余项合在一起乘以![]() ,然后根据上上面发现的结论进行计算即可.
,然后根据上上面发现的结论进行计算即可.
∵① x 1 x 1 x2 1 ;
② x 1x2 x 1 x3 1 ;
③ x 1x3 x2 x 1 x4 1 ;
…
∴(x-1)(xn+xn-1+xn-2+…+x+1)=xn+1-1,
∴ x 1x2019 x2018 x2017 x 1 ![]() ,
,
故答案为:x2020-1;
(1)原式= ![]() ×32019 32018 32017 … 3 1
×32019 32018 32017 … 3 1
=![]() ×(32020 1)
×(32020 1)
=![]() ;
;
(2)原式= 250 249 248 2 1 1
=![]() ×250 249 248 2 1] 1
×250 249 248 2 1] 1
=![]() ×251 11
×251 11
=![]() -
-![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动,设运动时间为x(秒),△PBQ的面只为y(cm2).
(1)求y关于x的函数关系式,并写出x的取值范围.
(2)求△PBQ的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明解不等式![]() 的过程如图,请指出他解答过程中错误步骤的序号,并写出正确的解答过程.
的过程如图,请指出他解答过程中错误步骤的序号,并写出正确的解答过程.
解:去分母,得3(1+x)-2(2x+1)≤1.①
去括号,得3+3x-4x+1≤1.②
移项,得3x-4x≤1-3-1.③
合并同类项,得-x≤-3.④
两边都除以-1,得x≤3.⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:分子、分母都是整式,并且分母中含有未知数的不等式叫做分式不等式.小亮在解分式不等式![]() 时,是这样思考的:根据“两数相除,同号得正,异号得负”,原分式不等式可转化为下面两个不等式组:①
时,是这样思考的:根据“两数相除,同号得正,异号得负”,原分式不等式可转化为下面两个不等式组:①![]() 或②
或②![]()
解不等式组①,得x>3,
解不等式组②,得![]() .
.
所以原分式不等式的解集为x>3或![]() .
.
探究:请你参考小亮思考问题的方法,解不等式![]() .
.
应用:不等式(x﹣3)(x+5)≤0的解集是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有16个只有颜色不同的球,其中红球有x个,白球有2x个,其他均为黄球,现甲从布袋中随机摸出一个球,若是红球则甲同学获胜,甲同学把摸出的球放回并搅匀,由乙同学随机摸出一个球,若为黄球,则乙同学获胜。
(1)当X=3时,谁获胜的可能性大?
(2)当x为何值时,游戏对双方是公平的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.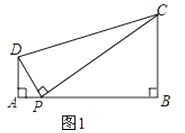
(1)求证:ADBC=APBP.
(2)探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.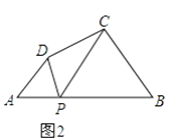
(3)应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=12,AD=BD=10.点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),当以D为圆心,以DC为半径的圆与AB相切,求t的值.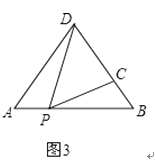
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
①求证:△BCE≌△ACD;
②求证:CF=CH;
③判断△CFH的形状并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合肥市某学校搬迁,教师和学生的寝室数量在增加,若该校今年准备建造三类不同的寝室,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2015年学校寝室数为64个,2017年建成后寝室数为121个,求2015至2017年的平均增长率;
(2)若建成后的寝室可供600人住宿,求单人间的数量;
(3)若该校今年建造三类不同的寝室的总数为180个,则该校的寝室建成后最多可供多少师生住宿?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com