
【题目】在平面直角坐标系中,B(2,0),A(6,6),M(0,6),P点为y轴上一动点。
(1)当P点在线段OM上运动时,试问是否存在一个点P使![]() =13,若存在,请求出P点耳朵坐标;若不存在,请说明理由.
=13,若存在,请求出P点耳朵坐标;若不存在,请说明理由.
(2)当点P在y的正半轴上运动时(不包括O,M),∠PAM,∠APB,∠PBO三者之间是否存在某种数量关系,如果有,请利用所学的知识找出并证明;如果没有,请说明理由。

【答案】(1)P(0,![]() );(2)当P在OM线段上,∠PAM+∠PBO=∠APB;当P在OM的延长线上,∠PAM+∠APB=∠PBO.
);(2)当P在OM线段上,∠PAM+∠PBO=∠APB;当P在OM的延长线上,∠PAM+∠APB=∠PBO.
【解析】
(1)设P(0,m).根据S△PAB=S梯形AMOB-S△APM-S△PBO,构建方程即可解决问题;
(2)分2种情形,分别画出图形,根据平行线的判定和性质解决问题即可.
(1)设P(0,m).
∵S△PAB=13,四边形AMOB是直角梯形,
∴![]() (6+2)6-
(6+2)6-![]() m2-
m2-![]() (6-m)6=13,
(6-m)6=13,
∴m=![]() ,
,
∴P(0,![]() ),
),
(2)①如图2-1中,当点P在线段OM上时,结论:∠APB+∠PBO=∠PAM;
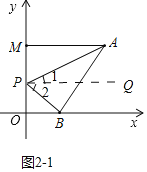
理由:作PQ∥AM,则PQ∥AM∥ON,
∴∠1=∠PAM,∠2=∠PBO,
∴∠1+∠2=∠PAM+∠PBO,
即∠APB=∠PAM+∠PBO,
∠APB+∠PBO=∠PAM;
②如图2-3中,当点P在OM的延长线上时,结论:∠PBO=∠PAM+∠APB.
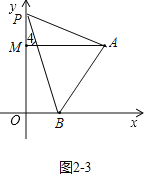
理由:∵AM∥OB,
∴∠4=∠PBO,
∵∠4=∠PAM+∠APB,
∴∠PBO=∠PAM+∠APB.
综合上述:当P在OM线段上,∠PAM+∠PBO=∠APB;当P在OM的延长线上,∠PAM+∠APB=∠PBO.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.

(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明解不等式![]() 的过程如图,请指出他解答过程中错误步骤的序号,并写出正确的解答过程.
的过程如图,请指出他解答过程中错误步骤的序号,并写出正确的解答过程.
解:去分母,得3(1+x)-2(2x+1)≤1.①
去括号,得3+3x-4x+1≤1.②
移项,得3x-4x≤1-3-1.③
合并同类项,得-x≤-3.④
两边都除以-1,得x≤3.⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有16个只有颜色不同的球,其中红球有x个,白球有2x个,其他均为黄球,现甲从布袋中随机摸出一个球,若是红球则甲同学获胜,甲同学把摸出的球放回并搅匀,由乙同学随机摸出一个球,若为黄球,则乙同学获胜。
(1)当X=3时,谁获胜的可能性大?
(2)当x为何值时,游戏对双方是公平的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.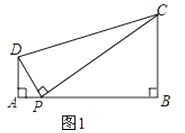
(1)求证:ADBC=APBP.
(2)探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.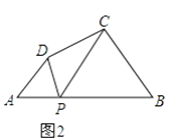
(3)应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=12,AD=BD=10.点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),当以D为圆心,以DC为半径的圆与AB相切,求t的值.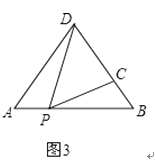
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=72°.

(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
①求证:△BCE≌△ACD;
②求证:CF=CH;
③判断△CFH的形状并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥CD,∠B=70°,∠BCE=20°,∠CEF=130°,请判断AB与EF的位置关系,并说明理由.
解: ,理由如下:
∵AB∥CD,
∴∠B=∠BCD,( )
∵∠B=70°,
∴∠BCD=70°,( )
∵∠BCE=20°,
∴∠ECD=50°,
∵∠CEF=130°,
∴ + =180°,
∴EF∥ ,( )
∴AB∥EF.( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区100个家庭收入按从高到低是5800,……,10000元各不相同,在输入计算时,把最大的数错误地输成100000元,则依据错误的数据算出的平均数比实际平均数多( )
A. 900元B. 942元C. 90000元D. 9000元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com