
【题目】阅读理解:在以后你的学习中,我们会学习一个定理:直角三角形斜边上的中线等于斜边的一半,即:如图1,在Rt△ABC中,∠ACB=90°,若点D是斜边AB的中点,则CD=![]() AB.
AB.
灵活应用:如图2,△ABC中,∠BAC=90°,AB=6,AC=8,点D是BC的中点,连接AD,将△ACD沿AD翻折得到△AED,连接BE,CE.
(1)填空:AD= ;
(2)求证:∠BEC=90°;
(3)求BE.

【答案】(1)5;(2)证明见解析;(3)![]() .
.
【解析】
(1)利用勾股定理求出BC,再利用阅读理解中的结论即可解决问题;
(2)由将△ACD沿AD翻折得到△AED,推出CD=DE=BD,推出∠DBE=∠DEB,∠DCE=∠DEC,由∠DBF+∠DEB+∠DEC+∠DCE=180°,推出2∠DEB+2∠DEC=180°,可得∠DEB+∠DEC=90°;
(3)如图2中,延长AD交EC于H.由△ACB∽△HAC,![]() =
=![]() ,求出AH,DH,再证明BE=2DH即可解决问题;
,求出AH,DH,再证明BE=2DH即可解决问题;
(1)解:在Rt△ABC中,∵∠BAC=90°,AB=6,AC=8,
∴BC=![]() =10,
=10,
∵BD=DC,
∴AD=![]() BC=5,
BC=5,
故答案为5;
(2)证明:∵将△ACD沿AD翻折得到△AED,
∴CD=DE=BD,
∴∠DBE=∠DEB,∠DCE=∠DEC,
∵∠DBF+∠DEB+∠DEC+∠DCE=180°,
∴2∠DEB+2∠DEC=180°,
∴∠DEB+∠DEC=90°,
∴∠BEC=90°;
(3)解:如图2中,延长AD交EC于H.
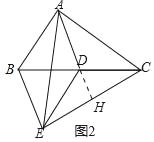
∵AE=AE,∠HAE=∠HAC,
∴AH⊥EC,
∴EH=CH,
∵BD=CD,
∴BE=2DH,
∵DA=DC,
∴∠ACB=∠CAH,
∵∠CAB=∠AHC=90°,
∴△ACB∽△HAC,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴AH=![]() ,
,
∴DH=AH﹣AD=![]() ﹣5=
﹣5=![]() ,
,
∴BE=2DH=![]() .
.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,点C,O,B在同一条直线上,∠AOB=90°,∠AOE=∠DOB,则下列结论:①∠EOD=90°;②∠COE=∠AOD;③∠AOE+∠DOC=180![]() ;④互余的角有4对.其中正确的有( )
;④互余的角有4对.其中正确的有( )
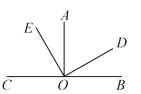
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为点G,连接CG,下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值 ![]() ﹣1.其中正确的说法有( )个.
﹣1.其中正确的说法有( )个.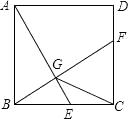
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机动车辆出发前油箱中有油![]() 升,行驶若干小时后,在途中加油站加油若干.油箱中余油量
升,行驶若干小时后,在途中加油站加油若干.油箱中余油量![]() (升)与行驶时间
(升)与行驶时间![]() (时)之间的关系如图,请根据图中给出的信息,解决下列问题.
(时)之间的关系如图,请根据图中给出的信息,解决下列问题.

(1)机动车辆行驶了 小时后加油,中途加油________升.
(2)加油后油箱中的油最多可行驶多少小时?
(3)若加油站距目的地还有![]() 公里,机动车每小时走
公里,机动车每小时走![]() 公里,油箱中的油能否使车到达目的地?
公里,油箱中的油能否使车到达目的地?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是规格为8×8的正方形网格,每个小方格都是边长为1的正方形.
(1)在网格中建立平面直角坐标系,使A点坐标为(﹣2,4);
(2)在第二象限内的格点(网格线的交点)上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是_____.
(3)画出△ABC关于y轴对称的△A′B′C′.
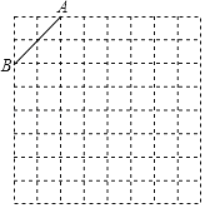
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,直线L:y=kx+5k与x轴负半轴、y轴正半轴分别交于A、B两点.
(1)当OA=OB时,试确定直线L解析式;
(2)在(1)的条件下,如图②所示,设Q为AB延长线上一点,连接OQ,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若BN=3,求MN的长;
(3)当K取不同的值时,点B在y轴正半轴上运动,分别以OB、AB为边在第一、第二象限作等腰直角△OBF和等腰直角△ABE,连EF交y轴于P点,问当点B在y轴上运动时,试猜想△ABP的面积是否改变,若不改变,请求出其值;若改变,请说明理由.
(4)当K取不同的值时,点B在y轴正半轴上运动,以AB为边在第二象限作等腰直角△ABE,则动点E在直线______上运动.(直接写出直线的表达式)



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写推理理由:
如图,CD∥EF,∠1=∠2,求证:∠3=∠ACB.
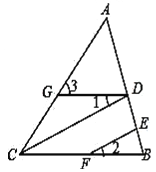
证明:∵CD∥EF,
∴∠DCB=∠2( ),
∵∠1=∠2,
∴∠DCB=∠1( ).
∴GD∥CB( ),
∴∠3=∠ACB( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com