
【题目】某机动车辆出发前油箱中有油![]() 升,行驶若干小时后,在途中加油站加油若干.油箱中余油量
升,行驶若干小时后,在途中加油站加油若干.油箱中余油量![]() (升)与行驶时间
(升)与行驶时间![]() (时)之间的关系如图,请根据图中给出的信息,解决下列问题.
(时)之间的关系如图,请根据图中给出的信息,解决下列问题.

(1)机动车辆行驶了 小时后加油,中途加油________升.
(2)加油后油箱中的油最多可行驶多少小时?
(3)若加油站距目的地还有![]() 公里,机动车每小时走
公里,机动车每小时走![]() 公里,油箱中的油能否使车到达目的地?
公里,油箱中的油能否使车到达目的地?
【答案】(1)![]() ;(2)加油后油箱中的油最多可行驶
;(2)加油后油箱中的油最多可行驶![]() 小时;(3)不能.
小时;(3)不能.
【解析】
(1)根据函数图象可以解答本题;
(2)根据函数图象中的数据可以解答本题;
(3)先判断,然后算出走260公里需要多少油,对比即可.
解:(1)由图可得,
机动车行驶了5小时后加油,加油36-12=24升,
故答案为:5,24;
(2)由图可得,
加油后油箱中的油最多可行驶:11-5=6小时,
即加油后油箱中的油最多可行驶6小时;
(3)要到达目的地,油箱中的油不够用,
理由:∵加油后油箱中的油最多可行驶6小时,260÷40=6.5,
6.5>6,
∴如果加油站距目的地还有260km,车速为40km/h,要到达目的地,油箱中的油不能使车到达目的地.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】已知∠α和∠β互补,且∠α>∠β,下列表示角的式子:①90°-∠β;②∠α-90°;③![]() (∠α+∠β);④
(∠α+∠β);④![]() (∠α-∠β).其中能表示∠β的余角的有( )个.
(∠α-∠β).其中能表示∠β的余角的有( )个.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=6,点F是AB的中点,E为BC边上一点,且EF⊥ED,连结DF,M为DF的中点,连结MA,ME.若AM⊥ME,则AE的长为( )
A.5
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:在以后你的学习中,我们会学习一个定理:直角三角形斜边上的中线等于斜边的一半,即:如图1,在Rt△ABC中,∠ACB=90°,若点D是斜边AB的中点,则CD=![]() AB.
AB.
灵活应用:如图2,△ABC中,∠BAC=90°,AB=6,AC=8,点D是BC的中点,连接AD,将△ACD沿AD翻折得到△AED,连接BE,CE.
(1)填空:AD= ;
(2)求证:∠BEC=90°;
(3)求BE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据所学知识完成小题:
(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等边△ABE和等边△ACD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.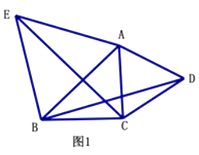
(2)【深入探究】如图2,△ABC中,∠ABC=45°,AB=5cm,BC=3cm,分别以AB、AC为边向外作正方形ABNE和正方形ACMD,连接BD,求BD的长.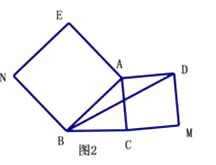
(3)如图3,在(2)的条件下,以AC为直角边在线段AC的左侧作等腰直角△ACD,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
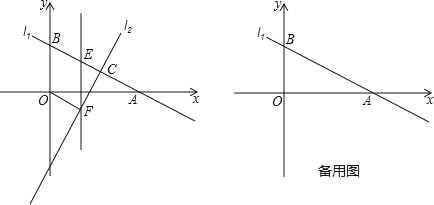
【题目】如图,直线![]() 分别与x轴、y轴交于
分别与x轴、y轴交于![]() 两点,与直线
两点,与直线![]() 交于点C(4,2).
交于点C(4,2).
(1)点A坐标为( , ),B为( , );
(2)在线段![]() 上有一点E,过点E作y轴的平行线交直线
上有一点E,过点E作y轴的平行线交直线![]() 于点F,设点E的横坐标为m,当m为何值时,四边形
于点F,设点E的横坐标为m,当m为何值时,四边形![]() 是平行四边形;
是平行四边形;
(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得![]() 四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com