
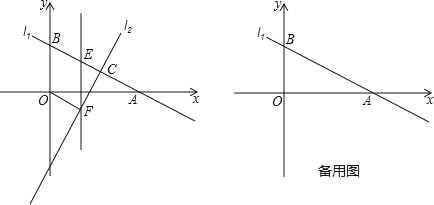
【题目】如图,直线![]() 分别与x轴、y轴交于
分别与x轴、y轴交于![]() 两点,与直线
两点,与直线![]() 交于点C(4,2).
交于点C(4,2).
(1)点A坐标为( , ),B为( , );
(2)在线段![]() 上有一点E,过点E作y轴的平行线交直线
上有一点E,过点E作y轴的平行线交直线![]() 于点F,设点E的横坐标为m,当m为何值时,四边形
于点F,设点E的横坐标为m,当m为何值时,四边形![]() 是平行四边形;
是平行四边形;
(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得![]() 四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
【答案】(1)(8,0);(0,4).(2)故当![]() 时,四边形
时,四边形![]() 是平行四边形;(3)Q点坐标为
是平行四边形;(3)Q点坐标为![]() 、
、![]() 、
、![]() 或
或![]() .
.
【解析】
(1)由点C的坐标利用待定系数法即可求出直线l1的解析式,再分别令直线![]() 的解析式中
的解析式中![]() 求出对应的y、x值,即可得出点A、B的坐标;
求出对应的y、x值,即可得出点A、B的坐标;
(2)由点C的坐标利用待定系数法即可求出直线![]() 的解析式,结合点E的横坐标即可得出点E、F的坐标,再根据平行四边形的性质即可得出关于m的一元一次方程,解方程即可得出结论;
的解析式,结合点E的横坐标即可得出点E、F的坐标,再根据平行四边形的性质即可得出关于m的一元一次方程,解方程即可得出结论;
(3)分![]() 为边和
为边和![]() 为对角线两种情况讨论.当
为对角线两种情况讨论.当![]() 为边时,根据菱形的性质找出点P的坐标,结合A、B的坐标即可得出点Q的坐标;当
为边时,根据菱形的性质找出点P的坐标,结合A、B的坐标即可得出点Q的坐标;当![]() 为对角线时,根据三角形相似找出点P的坐标,再根据菱形对角线互相平分即可得出点Q的坐标.综上即可得出结论.
为对角线时,根据三角形相似找出点P的坐标,再根据菱形对角线互相平分即可得出点Q的坐标.综上即可得出结论.
解:(1)将点C(4,2)代入![]() 中,
中,
得:![]() ,解得:
,解得:![]() ,
,
∴直线![]() 为
为![]() .
.
令![]() 中
中![]() ,则
,则![]() ,
,
∴B(0,4);
令![]() 中
中![]() ,则
,则![]() ,
,
∴A(8,0).
(2)∵点C(4,2)是直线![]() 上的点,
上的点,
∴![]() ,解得:
,解得:![]() ,
,
∴直线![]() 为
为![]() .
.
∵点E的横坐标为![]() ,
,
∴![]() ,
,
∴![]() .
.
∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,即
,即![]() ,
,
解得:![]() .
.
故当![]() 时,四边形
时,四边形![]() 是平行四边形.
是平行四边形.
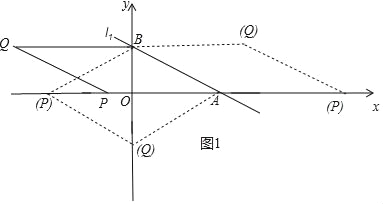
(3)假设存在.
以![]() 为顶点的菱形分两种情况:
为顶点的菱形分两种情况:
①以![]() 为边,如图1所示.
为边,如图1所示.
∵点A(8,0),B(0,4),
∴![]() .
.
∵以![]() 为顶点的四边形为菱形,
为顶点的四边形为菱形,
∴![]() 或
或![]() .
.
当![]() 时,
时,![]() 或
或![]() ;
;
当![]() 时,点P(﹣8,0).
时,点P(﹣8,0).
当![]() 时,
时,![]() ,即
,即![]() ;
;
当P(![]() )时,
)时,![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() .
.
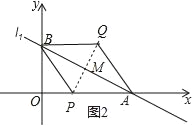
②以![]() 为对角线,对角线的交点为M,如图2所示.
为对角线,对角线的交点为M,如图2所示.
∵点![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() ,即(3,0).
,即(3,0).
∵以![]() 为顶点的四边形为菱形,
为顶点的四边形为菱形,
∴点![]() ,即(5,4).
,即(5,4).
综上可知:若点P为x轴上一点,则在平面直角坐标系中存在一点Q,使得![]() 四个点能构成一个菱形,此时Q点坐标为
四个点能构成一个菱形,此时Q点坐标为![]() 、
、![]() 、
、![]() 或
或![]() .
.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
【题目】某机动车辆出发前油箱中有油![]() 升,行驶若干小时后,在途中加油站加油若干.油箱中余油量
升,行驶若干小时后,在途中加油站加油若干.油箱中余油量![]() (升)与行驶时间
(升)与行驶时间![]() (时)之间的关系如图,请根据图中给出的信息,解决下列问题.
(时)之间的关系如图,请根据图中给出的信息,解决下列问题.

(1)机动车辆行驶了 小时后加油,中途加油________升.
(2)加油后油箱中的油最多可行驶多少小时?
(3)若加油站距目的地还有![]() 公里,机动车每小时走
公里,机动车每小时走![]() 公里,油箱中的油能否使车到达目的地?
公里,油箱中的油能否使车到达目的地?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据表中的信息判断,下列语句中正确的是

( )
A.![]() =1.59
=1.59
B.235的算术平方根比15.3小
C.只有3个正整数n满足![]()
D.根据表中数据的变化趋势,可以推断出16.12将比256增大3.19
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写推理理由:
如图,CD∥EF,∠1=∠2,求证:∠3=∠ACB.
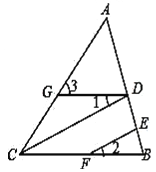
证明:∵CD∥EF,
∴∠DCB=∠2( ),
∵∠1=∠2,
∴∠DCB=∠1( ).
∴GD∥CB( ),
∴∠3=∠ACB( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
一般地,n个相同的因数a相乘![]() 记为an,记为an.如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
记为an,记为an.如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
(1)计算以下各对数的值:
log24= ,log216= ,log264= .
(2)观察(1)中三数4、16、64之间满足怎样的关系式,log24、log216、log264之间又满足怎样的关系式 .
(3)由(2)的结果,你能归纳出一个一般性的结论吗?
logaM+logaN= ;(a>0且a≠1,M>0,N>0)
(4)根据幂的运算法则:anam=an+m以及对数的含义证明上述结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都市的水费实行下表的收费方式:
每月用水量 | 单价 |
不超出 | 2元/ |
超出 | 3元/ |
超出 | 4元/ |
(1)周老师家九月份用了![]() 的水,应付多少水费?
的水,应付多少水费?
(2)如果李老师家九月份的用水量为![]() ,那么应付的水费为多少元?
,那么应付的水费为多少元?
(3)如果曹老师家九月和十月一共用了![]() 的水,且已知九月比十月少,设九月用水量为
的水,且已知九月比十月少,设九月用水量为![]() ,那么曹老师这两个月一共要交多少钱的水费?(可用含
,那么曹老师这两个月一共要交多少钱的水费?(可用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com