
【题目】如图,弦AB的长等于⊙O的半径,那么弦AB所对的圆周角的度数 . 
【答案】30°或150°
【解析】在优弧上取点C,连接AC、BC;在劣弧上取点D,连接AD、BD,
∵弦AB的长等于⊙O的半径,
∴△ABO是等边三角形,
∴∠AOB=60°,
∴∠ACB=![]() ∠AOB=30°,
∠AOB=30°,
∴∠ADB=180°-∠ACB=150°,
所以答案是:30°或150°.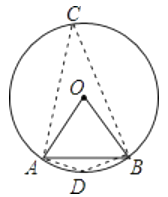
【考点精析】根据题目的已知条件,利用圆周角定理和圆内接四边形的性质的相关知识可以得到问题的答案,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】根据所学知识完成小题:
(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等边△ABE和等边△ACD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.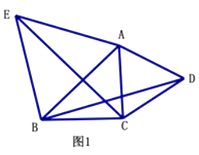
(2)【深入探究】如图2,△ABC中,∠ABC=45°,AB=5cm,BC=3cm,分别以AB、AC为边向外作正方形ABNE和正方形ACMD,连接BD,求BD的长.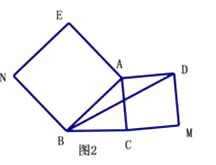
(3)如图3,在(2)的条件下,以AC为直角边在线段AC的左侧作等腰直角△ACD,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=6,OB=8,OC=10,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为8;③S四边形AOBO′=24+12![]() ;④S△AOC+S△AOB=24+9
;④S△AOC+S△AOB=24+9![]() ;⑤S△ABC=36+25
;⑤S△ABC=36+25![]() ; 其中正确的结论有( )
; 其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
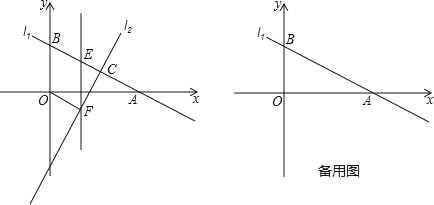
【题目】如图,直线![]() 分别与x轴、y轴交于
分别与x轴、y轴交于![]() 两点,与直线
两点,与直线![]() 交于点C(4,2).
交于点C(4,2).
(1)点A坐标为( , ),B为( , );
(2)在线段![]() 上有一点E,过点E作y轴的平行线交直线
上有一点E,过点E作y轴的平行线交直线![]() 于点F,设点E的横坐标为m,当m为何值时,四边形
于点F,设点E的横坐标为m,当m为何值时,四边形![]() 是平行四边形;
是平行四边形;
(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得![]() 四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com