【题目】如图，△ABC的内心在y轴上，点C的坐标为（2，0），点B的坐标为（0，2），直线AC的解析式为： y=
x1 ，则tanA的值是 ． 
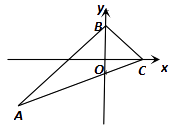
【答案】
【解析】∵△ABC的内心在y轴上，
∴∠ABO=∠CBO，
又∵C（2，0），B（0，2），
∴BO=CO，BC=2
，
∴∠BCO=∠CBO=45°，
∴∠ABC=90°，
又∵直线AC的解析式为： y=
x1 ，
∴设A（x，x1 ），
∴AB2=x2+（x3）2，AC2=（x-2）2+（x1 ）2，
∴AB2+BC2=AC2，
∴x2+（x3）2+8=（x-2）2+（x1 ）2，
∴x=-6，
∴y=-4，
∴A（-6，-4），
∴AB=6，
∴tanA=
=
=.
所以答案是：.
【考点精析】利用勾股定理的概念和锐角三角函数的定义对题目进行判断即可得到答案，需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数．
阳光课堂同步练习系列答案科目：初中数学 来源： 题型：
【题目】如图是规格为8×8的正方形网格，每个小方格都是边长为1的正方形．
(1)在网格中建立平面直角坐标系，使A点坐标为(﹣2，4)；
(2)在第二象限内的格点(网格线的交点)上画一点C，使点C与线段AB组成一个以AB为底的等腰三角形，且腰长是无理数，则C点坐标是_____．
(3)画出△ABC关于y轴对称的△A′B′C′．
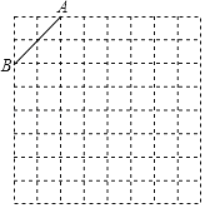
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①所示，直线L：y＝kx+5k与x轴负半轴、y轴正半轴分别交于A、B两点．
(1)当OA＝OB时，试确定直线L解析式；
(2)在(1)的条件下，如图②所示，设Q为AB延长线上一点，连接OQ，过A、B两点分别作AM⊥OQ于M，BN⊥OQ于N，若BN＝3，求MN的长；
(3)当K取不同的值时，点B在y轴正半轴上运动，分别以OB、AB为边在第一、第二象限作等腰直角△OBF和等腰直角△ABE，连EF交y轴于P点，问当点B在y轴上运动时，试猜想△ABP的面积是否改变，若不改变，请求出其值；若改变，请说明理由．
(4)当K取不同的值时，点B在y轴正半轴上运动，以AB为边在第二象限作等腰直角△ABE，则动点E在直线______上运动．(直接写出直线的表达式)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图.已知曲线是由顶点为T的二次函数 
的图象旋转45度得到，直线AB： 
交曲线于C，D两点.
（1）线段AT长为,
（2）在y轴上有一点P，且PC+PD 为最小，则点P的坐标为
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】填写推理理由：
如图，CD∥EF，∠1=∠2，求证：∠3=∠ACB．
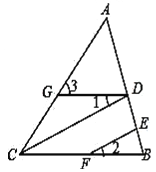
证明：∵CD∥EF，
∴∠DCB=∠2（ ），
∵∠1=∠2，
∴∠DCB=∠1（ ）．
∴GD∥CB（ ），
∴∠3=∠ACB（ ）．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
