
【题目】如图,O是正△ABC内一点,OA=6,OB=8,OC=10,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为8;③S四边形AOBO′=24+12![]() ;④S△AOC+S△AOB=24+9
;④S△AOC+S△AOB=24+9![]() ;⑤S△ABC=36+25
;⑤S△ABC=36+25![]() ; 其中正确的结论有( )
; 其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
【答案】D
【解析】①∵△ABC为正三角形,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,
∴∠OBO′=∠ABC=60°,OB=O′B,AB=BC,
即∠1+∠2=∠2+∠3=60°,
∴∠1=∠3,
在△BO′A和△BOC中,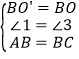 ,
,
∴△BO′A≌△BOC,
又∵∠OBO′=60°,
∴△BO′A可以由△BOC绕点B逆时针旋转60°得到;
故①正确;
②如图1:连接OO′,
∵将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,
∴∠OBO′=60°,OB=O′B,
∴△OBO′为正三角形,
又∵OB=8,
∴OO′=8;
故②正确;
③由①知△BO′A≌△BOC,
∵OC=10,
∴AO′=CO=10,
∴AO′2=AO2+OO′2,
∴△AOO′为直角三角形,
∴S四边形AOBO′=S△AOO′+S△BOO′=![]() ×6×8+
×6×8+![]() ×8×4
×8×4![]() =24+16
=24+16![]() ;
;
故③错误;
④如图2,将△AOB绕点A逆时针旋转60°,使AB与AC重合,点O旋转至O′′,
∴∠OAO′′=60°,OA=O′′A,OB=O′′C,
∵OA=6,
∴△AOO′′是边长为6的正三角形,
又∵OB=8,OC=10,
∴O′′C=8,
∴OC2=OO′′2+O′′C2,
∴△COO′′为直角三角形,
∴S△AOC+S△AOB=S△AOC+S△AO′′C=S△O′′OC+S△AO′′O=![]() ×6×8+
×6×8+![]() ×6×3
×6×3![]() =24+9
=24+9![]() ,
,
故④正确;
⑤S△AOB=![]() ×6×8×
×6×8×![]() =12,
=12,
∴S△ABC=S△AOB+S△AOC+S△BOC=S△AOB+S△ABO′+S△AOC=S△AOO′+S△BOO′+S△O′′OC+S△AO′′O-S△AOB=24+16![]() +24+9
+24+9![]() -12=36+25
-12=36+25![]() ;
;
故⑤正确;
综上所述正确的结论有:①②④⑤.
所以答案是:D.
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高,以及对勾股定理的逆定理的理解,了解如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.


科目:初中数学 来源: 题型:
【题目】平面内的两条直线有相交和平行两种位置关系.




(1)如图1,若![]() ,点
,点![]() 在
在![]() 外部,则有
外部,则有![]() ,又可证
,又可证![]() ,得
,得![]() ,将点
,将点![]() 移到
移到![]() 内部,如图2,以上结论是否成立?若成立,说明理由;若不成立,则
内部,如图2,以上结论是否成立?若成立,说明理由;若不成立,则![]() 之间有何数量关系?请证明你的结论;
之间有何数量关系?请证明你的结论;
(2)在如图2中,将直线![]() 绕点
绕点![]() 逆时针方向旋转一定角度交直线
逆时针方向旋转一定角度交直线![]() 于点
于点![]() 如图3,则
如图3,则![]()
![]() 之间有何数量关系? (不需证明);
之间有何数量关系? (不需证明);
(3)根据(2)的结论,求如图4中![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图:若![]() ,点
,点![]() 在
在![]() 、
、![]() 内部,则
内部,则![]() 、
、![]() 、
、![]() 之间有何数量关系?请证明你的结论.
之间有何数量关系?请证明你的结论.

(2)如图,若![]() ,将点
,将点![]() 移到
移到![]() 、
、![]() 外部,则
外部,则![]() 、
、![]() 、
、![]() 的数量关系是______.
的数量关系是______.

(3)在下图中,将直线![]() 绕点
绕点![]() 逆时针方向旋转一定角度交直线
逆时针方向旋转一定角度交直线![]() 于点
于点![]() ,则
,则![]() 、
、![]() 、
、![]() 、
、![]() 之间满足的数量关系是______.
之间满足的数量关系是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC中,AC=BC>3,点M在AC上,点N在CB的延长线上,MN交AB于点O,且AM=BN=3,则S△AMO与S△BNO的差是( )
A.9
B.4.5
C.0
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
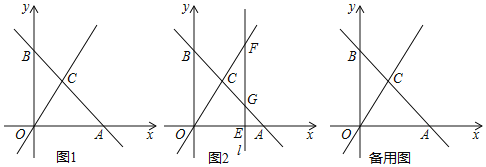
【题目】如图1,平面直角坐标系中,直线![]() 与直线
与直线![]() 交与点
交与点![]() .
.
![]() 轴上是否存在点P,使
轴上是否存在点P,使![]() 的面积是
的面积是![]() 面积的二倍?若存在,直接写出点P的坐标;若不存在,说明理由.
面积的二倍?若存在,直接写出点P的坐标;若不存在,说明理由.
![]() 如图2,若点E是x轴上的一个动点,点E的横坐标为
如图2,若点E是x轴上的一个动点,点E的横坐标为![]() ,过点E作直线
,过点E作直线![]() 轴于点E,交直线
轴于点E,交直线![]() 于点F,交直线
于点F,交直线![]() 于点G,求m为何值时,
于点G,求m为何值时,![]() ≌
≌![]() ?请说明理由.
?请说明理由.
![]() 在
在![]() 的前提条件下,直线l上是否存在点Q,使
的前提条件下,直线l上是否存在点Q,使![]() 的值最小?若存在,直接写出点Q的坐标;若不存在,说明理由.
的值最小?若存在,直接写出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据表中的信息判断,下列语句中正确的是

( )
A.![]() =1.59
=1.59
B.235的算术平方根比15.3小
C.只有3个正整数n满足![]()
D.根据表中数据的变化趋势,可以推断出16.12将比256增大3.19
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+bx+c经过A(﹣1,0),C(2,﹣3)两点,与y轴交于点D,与x轴交于另一点B.
x2+bx+c经过A(﹣1,0),C(2,﹣3)两点,与y轴交于点D,与x轴交于另一点B.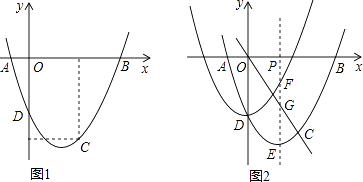
(1)求此抛物线的解析式及顶点坐标;
(2)若将此抛物线平移,使其顶点为点D,需如何平移?写出平移后抛物线的解析式;
(3)过点P(m,0)作x轴的垂线(1≤m≤2),分别交平移前后的抛物线于点E,F,交直线OC于点G,求证:PF=EG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com