
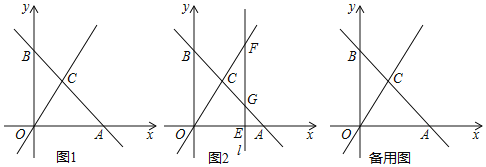
【题目】如图1,平面直角坐标系中,直线![]() 与直线
与直线![]() 交与点
交与点![]() .
.
![]() 轴上是否存在点P,使
轴上是否存在点P,使![]() 的面积是
的面积是![]() 面积的二倍?若存在,直接写出点P的坐标;若不存在,说明理由.
面积的二倍?若存在,直接写出点P的坐标;若不存在,说明理由.
![]() 如图2,若点E是x轴上的一个动点,点E的横坐标为
如图2,若点E是x轴上的一个动点,点E的横坐标为![]() ,过点E作直线
,过点E作直线![]() 轴于点E,交直线
轴于点E,交直线![]() 于点F,交直线
于点F,交直线![]() 于点G,求m为何值时,
于点G,求m为何值时,![]() ≌
≌![]() ?请说明理由.
?请说明理由.
![]() 在
在![]() 的前提条件下,直线l上是否存在点Q,使
的前提条件下,直线l上是否存在点Q,使![]() 的值最小?若存在,直接写出点Q的坐标;若不存在,说明理由.
的值最小?若存在,直接写出点Q的坐标;若不存在,说明理由.
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
![]() 利用一次函数图象上点的坐标特征可求出点A的坐标,由
利用一次函数图象上点的坐标特征可求出点A的坐标,由![]() 和
和![]() 等高且
等高且![]() 的面积是
的面积是![]() 面积的二倍,可得出
面积的二倍,可得出![]() ,进而可得出点P的坐标;
,进而可得出点P的坐标;
![]() 由
由![]() 可得出
可得出![]() ∽
∽![]() ,利用一次函数图象上点的坐标特征可求出点B的坐标,若要
,利用一次函数图象上点的坐标特征可求出点B的坐标,若要![]() ≌
≌![]() ,只需
,只需![]() ,即点C为线段BG的中点,结合点B,C的坐标可得出点G的坐标,再由
,即点C为线段BG的中点,结合点B,C的坐标可得出点G的坐标,再由![]() 轴可得出m的值;
轴可得出m的值;
![]() 作点O关于直线l对称的对称点D,连接BD,交直线l于点Q,此时
作点O关于直线l对称的对称点D,连接BD,交直线l于点Q,此时![]() 的值最小,由点O的坐标及直线l的解析式可得出点D的坐标,由点B,D的坐标,利用待定系数法求出直线BD的解析式,再利用一次函数图象上点的坐标特征即可求出点Q的坐标.
的值最小,由点O的坐标及直线l的解析式可得出点D的坐标,由点B,D的坐标,利用待定系数法求出直线BD的解析式,再利用一次函数图象上点的坐标特征即可求出点Q的坐标.
解:![]() 当
当![]() 时,
时,![]() ,
,
解得:![]() ,
,![]() 点A的坐标为
点A的坐标为![]() ,
,![]() .
.![]() 和
和![]() 等高,且
等高,且![]() 的面积是
的面积是![]() 面积的二倍,
面积的二倍,![]() ,
,![]() 点P的坐标为
点P的坐标为![]() 或
或![]() .
.![]() ,
,![]() ,
,![]() ,
,![]() ∽
∽![]() .
.
当![]() 时,
时,![]() ,
,![]() 点B的坐标为
点B的坐标为![]() .
.
若要![]() ≌
≌![]() ,只需
,只需![]() .
.![]() 点B的坐标为
点B的坐标为![]() ,点C的坐标为
,点C的坐标为![]() ,
,![]() 点G的坐标为
点G的坐标为![]() .
.
又![]() 轴,
轴,![]() .
.![]() 当
当![]() 时,
时,![]() ≌
≌![]() .
.![]() 由
由![]() 可知,直线l的解析式为
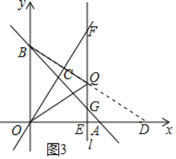
可知,直线l的解析式为![]() ,作点O关于直线l对称的对称点D,连接BD,交直线l于点Q,如图3所示.
,作点O关于直线l对称的对称点D,连接BD,交直线l于点Q,如图3所示.
![]() 点O,D关于直线l对称,
点O,D关于直线l对称,![]() ,点D的坐标为
,点D的坐标为![]() .
.![]() ,Q,D共线,
,Q,D共线,![]() 此时
此时![]() 取得最小值.
取得最小值.
设直线BD的解析式为![]() ,
,
将![]() ,
,![]() 代入
代入![]() ,得:
,得:![]() ,
,
解得: ,
,![]() 直线BD的解析式为
直线BD的解析式为![]() .
.
当![]() 时,
时,![]() ,
,![]() 直线l上存在点Q,使
直线l上存在点Q,使![]() 的值最小,点Q的坐标为
的值最小,点Q的坐标为![]() .
.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=6,OB=8,OC=10,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为8;③S四边形AOBO′=24+12![]() ;④S△AOC+S△AOB=24+9
;④S△AOC+S△AOB=24+9![]() ;⑤S△ABC=36+25
;⑤S△ABC=36+25![]() ; 其中正确的结论有( )
; 其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图的折线OPQ和线段EF,分表表示甲、乙两人与A地的距离![]() 、
、![]() 与他们所行时间
与他们所行时间![]() 之间的函数关系,且OP与EF相交于点M.
之间的函数关系,且OP与EF相交于点M.
![]() 求线段OP对应的
求线段OP对应的![]() 与x的函数关系式;
与x的函数关系式;
![]() 求
求![]() 与x的函数关系式以及A,B两地之间的距离;
与x的函数关系式以及A,B两地之间的距离;
![]() 求经过多少小时,甲、乙两人相距3km.
求经过多少小时,甲、乙两人相距3km.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)
平面直角坐标系中,点P(x,y)的横坐标x的绝对值表示为|x|,纵坐标y的绝对值表示为|y|,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为[P],即[P]=|x|+|y|(其中的“+“是四则运算中的加法),例如点P(1,2)的勾股值[P]=|1|+|2|=3.
(解决问题)
(1)求点A(-2.4),B(![]() +
+![]() -
-![]() )的勾股值[A],[B];
)的勾股值[A],[B];
(2)若点M在x轴的上方,其横,纵坐标均为整数,且[M]=3,请直接写出点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com