
【题目】如图,等腰直角△ABC中,AC=BC>3,点M在AC上,点N在CB的延长线上,MN交AB于点O,且AM=BN=3,则S△AMO与S△BNO的差是( )
A.9
B.4.5
C.0
D.无法确定
【答案】B
【解析】设AC=BC=a,
∵AM=BN=3,
∴CM=a-3,CN=a+3,
∴S△AMO=S△ABC-S四边形OBCM,S△BNO=S△CMN-S四边形OBCM,
∴S△AMO-S△BNO=S△ABC-S四边形OBCM-(S△CMN-S四边形OBCM),
=S△ABC-S△CMN,
=![]() ×BC×AC-
×BC×AC-![]() ×CN×CM,
×CN×CM,
=![]() ×a×a-
×a×a-![]() ×(a+3)×(a-3),
×(a+3)×(a-3),
=![]() ×a2-
×a2-![]() ×(a2-9),
×(a2-9),
=![]() ×a2-
×a2-![]() ×a2+
×a2+![]() ,
,
=![]() .
.
所以答案是:B.
【考点精析】本题主要考查了等腰直角三角形和三角形的面积的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;三角形的面积=1/2×底×高才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,D是AC上一点,E是AB上一点,且∠AED=∠C.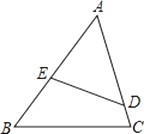
(1)求证:△AED∽△ACB;
(2)若AB=6,AD=4,AC=5,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知E、F分别为正方形ABCD的边BC、CD上的点,且∠EAF=45°.
(1)如图①求证:BE+DF=EF;
(2)连接BD分别交AE、AF于M、N,
①如图②,若AB=6![]() ,BM=3,求MN.
,BM=3,求MN.
②如图③,若EF∥BD,求证:MN=CE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=6,OB=8,OC=10,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为8;③S四边形AOBO′=24+12![]() ;④S△AOC+S△AOB=24+9
;④S△AOC+S△AOB=24+9![]() ;⑤S△ABC=36+25
;⑤S△ABC=36+25![]() ; 其中正确的结论有( )
; 其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图的折线OPQ和线段EF,分表表示甲、乙两人与A地的距离![]() 、
、![]() 与他们所行时间
与他们所行时间![]() 之间的函数关系,且OP与EF相交于点M.
之间的函数关系,且OP与EF相交于点M.
![]() 求线段OP对应的
求线段OP对应的![]() 与x的函数关系式;
与x的函数关系式;
![]() 求
求![]() 与x的函数关系式以及A,B两地之间的距离;
与x的函数关系式以及A,B两地之间的距离;
![]() 求经过多少小时,甲、乙两人相距3km.
求经过多少小时,甲、乙两人相距3km.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)
平面直角坐标系中,点P(x,y)的横坐标x的绝对值表示为|x|,纵坐标y的绝对值表示为|y|,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为[P],即[P]=|x|+|y|(其中的“+“是四则运算中的加法),例如点P(1,2)的勾股值[P]=|1|+|2|=3.
(解决问题)
(1)求点A(-2.4),B(![]() +
+![]() -
-![]() )的勾股值[A],[B];
)的勾股值[A],[B];
(2)若点M在x轴的上方,其横,纵坐标均为整数,且[M]=3,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;
(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com