
【题目】已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;
(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.

【答案】(1)证明见解析;(2)BE=AF,证明见解析.
【解析】(1)连接AD,根据等腰三角形的性质可得出AD=BD、∠EBD=∠FAD,根据同角的余角相等可得出∠BDE=∠ADF,由此即可证出△BDE≌△ADF(ASA),再根据全等三角形的性质即可证出BE=AF;
(2)连接AD,根据等腰三角形的性质及等角的补角相等可得出∠EBD=∠FAD、BD=AD,根据同角的余角相等可得出∠BDE=∠ADF,由此即可证出△EDB≌△FDA(ASA),再根据全等三角形的性质即可得出BE=AF.
详(1)证明:连接AD,如图①所示.

∵∠A=90°,AB=AC,
∴△ABC为等腰直角三角形,∠EBD=45°.
∵点D为BC的中点,
∴AD=![]() BC=BD,∠FAD=45°.
BC=BD,∠FAD=45°.
∵∠BDE+∠EDA=90°,∠EDA+∠ADF=90°,
∴∠BDE=∠ADF.
在△BDE和△ADF中,
 ,
,
∴△BDE≌△ADF(ASA),
∴BE=AF;
(2)BE=AF,证明如下:
连接AD,如图②所示.

∵∠ABD=∠BAD=45°,
∴∠EBD=∠FAD=135°.
∵∠EDB+∠BDF=90°,∠BDF+∠FDA=90°,
∴∠EDB=∠FDA.
在△EDB和△FDA中,
 ,
,
∴△EDB≌△FDA(ASA),
∴BE=AF.


科目:初中数学 来源: 题型:
【题目】小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员 | 小丽 | 小华 |
月销售件数(件) | 200 | 150 |
月总收入(元) | 1400 | 1250 |
假设营业员的月基本工资为x元,销售每件服装奖励y元.
(1)求x、y的值;
(2)若营业员小丽某月的总收入不低于1800元,那么小丽当月至少要卖服装多少件?
(3)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲3件,乙2件,丙1件共需315元;如果购买甲1件,乙2件,丙3件共需285元.某顾客想购买甲、乙、丙各一件共需 元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列关系式中正确的是( )
A.ac>0
B.b+2a<0
C.b2﹣4ac>0
D.a﹣b+c<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=﹣x2+bx+c的图象过点(﹣1,﹣8),(0,﹣3).
(1)求此二次函数的表达式,并用配方法将其化为y=a(x﹣h)2+k的形式;
(2)画出此函数图象的示意图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列命题中:①过一点有且只有一条直线与已知直线平行;②平方根与立方根相等的数有![]() 和
和![]() ;③在同一平面内,如果
;③在同一平面内,如果![]() ,
,![]() ,则
,则![]() ;④直线
;④直线![]() 外一点
外一点![]() 与直线
与直线![]() 上各点连接而成的所有线段中,最短线段的长是
上各点连接而成的所有线段中,最短线段的长是![]() ,则点
,则点![]() 到直线
到直线![]() 的距离是
的距离是![]() ;⑤无理数包括正无理数、零和负无理数.其中真命题的个数是( )
;⑤无理数包括正无理数、零和负无理数.其中真命题的个数是( )
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
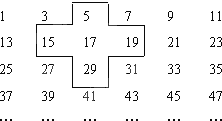
【题目】将连续的奇数1,3,5,7,…排成如图的数表,用如图所示的“十字框”可以框出5个数,这5个数之间将满足一定的关系,按照此方法,若“十字框”框出的5个数的和等于2015,则这5个数中最大数为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com