
【题目】已知:二次函数y=﹣x2+bx+c的图象过点(﹣1,﹣8),(0,﹣3).
(1)求此二次函数的表达式,并用配方法将其化为y=a(x﹣h)2+k的形式;
(2)画出此函数图象的示意图.
【答案】
(1)解:∵二次函数y=﹣x2+bx+c的图象过点(﹣1,﹣8),(0,﹣3),
∴ ![]() ,解得
,解得 ![]() ,
,
∴此二次函数的表达式为y=﹣x2+4x﹣3;
y=﹣x2+4x﹣3=﹣(x﹣2)2+1
(2)解:∵y=﹣(x﹣2)2+1,
∴顶点坐标为(2,1),对称轴方程为x=2.
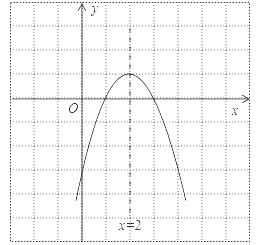
∵函数二次函数y=﹣x2+4x﹣3的开口向下,顶点坐标为(2,1),与x轴的交点为(3,0),(1,0),
∴其图象为
【解析】(1)利用待定系数法将已知点的坐标代入函数解析式,建立方程组,求出b、c的值,可得到而此函数解析式,再将其通过配方化成顶点式。
(2)先根据函数解析式求出抛物线与x轴的两交点坐标,再根据顶点坐标及抛物线的开口方向,画出函数图像。
【考点精析】通过灵活运用二次函数的图象和抛物线与坐标轴的交点,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某书店老板去图书批发市场购买某种图书.第一次用1200元购书若干本,并按该书定价7元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用1500元所购该书数量比第一次多10本.当按定价7元售出150本时,出现滞销,便以定价的5折售完剩余的书.
(1)每本书第一次的批发价是多少钱?
(2)试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;
(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解方程:![]()
(2)计算:3a(2a2-9a+3)-4a(2a-1)
(3)计算:(![]() )×(
)×(![]() )+|
)+|![]() -1|+(5-2π)0
-1|+(5-2π)0
(4)先化简,再求值:(xy2+x2y)![]() ,其中x=
,其中x=![]() ,y=
,y=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,从边长为a的正方形纸片中减去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸拼成如图2的等腰梯形(其面积= ![]() ).
).
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2,请直接用含a、b的式子表示S1和S2;
(2)请写出上述过程所揭示的乘法公式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,将线段
,将线段![]() 向右平移
向右平移![]() 个单位长度得到线段
个单位长度得到线段![]() (点
(点![]() 和点
和点![]() 分别是点
分别是点![]() 和点
和点![]() 的对应点),连接
的对应点),连接![]() 、
、![]() ,点
,点![]() 是线段
是线段![]() 的中点.
的中点.

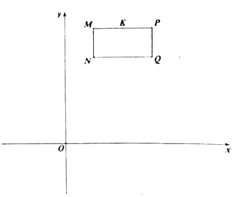
备用图
(1)求点![]() 的坐标;
的坐标;
(2)若长方形![]() 以每秒
以每秒![]() 个单位长度的速度向正下方运动,(点
个单位长度的速度向正下方运动,(点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分别是点
分别是点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的对应点),当
的对应点),当![]() 与
与![]() 轴重合时停止运动,连接
轴重合时停止运动,连接![]() 、
、![]() ,设运动时间为
,设运动时间为![]() 妙,请用含
妙,请用含![]() 的式子表示三角形
的式子表示三角形![]() 的面积
的面积![]() (不要求写出
(不要求写出![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,连接![]() 、
、![]() ,问是否存在某一时刻
,问是否存在某一时刻![]() ,使三角形
,使三角形![]() 的面积等于三角形
的面积等于三角形![]() 的面积?若存在,请求出
的面积?若存在,请求出![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:
如果y′= ![]() ,那么称点Q为点P的“关联点”.
,那么称点Q为点P的“关联点”.
例如:点(5,6)的“关联点”为点(5,6),点(﹣5,6)的“关联点”
为点(﹣5,﹣6).
(1)①点(2,1)的“关联点”为;②如果点A(3,﹣1),B(﹣1,3)的“关联点”中有一个在函数 ![]() 的图象上,那么这个点是(填“点A”或“点B”).
的图象上,那么这个点是(填“点A”或“点B”).
(2)①如果点M*(﹣1,﹣2)是一次函数y=x+3图象上点M的“关联点”,
那么点M的坐标为;②如果点N*(m+1,2)是一次函数y=x+3图象上点N的“关联点”,求点N的坐标 .
(3)如果点P在函数y=﹣x2+4(﹣2<x≤a)的图象上,其“关联点”Q的纵坐标
y′的取值范围是﹣4<y′≤4,那么实数a的取值范围是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com