
【题目】在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:
如果y′= ![]() ,那么称点Q为点P的“关联点”.
,那么称点Q为点P的“关联点”.
例如:点(5,6)的“关联点”为点(5,6),点(﹣5,6)的“关联点”
为点(﹣5,﹣6).
(1)①点(2,1)的“关联点”为;②如果点A(3,﹣1),B(﹣1,3)的“关联点”中有一个在函数 ![]() 的图象上,那么这个点是(填“点A”或“点B”).
的图象上,那么这个点是(填“点A”或“点B”).
(2)①如果点M*(﹣1,﹣2)是一次函数y=x+3图象上点M的“关联点”,
那么点M的坐标为;②如果点N*(m+1,2)是一次函数y=x+3图象上点N的“关联点”,求点N的坐标 .
(3)如果点P在函数y=﹣x2+4(﹣2<x≤a)的图象上,其“关联点”Q的纵坐标
y′的取值范围是﹣4<y′≤4,那么实数a的取值范围是 . 
【答案】
(1)(2,1),B
(2)(﹣1,2),(﹣1,﹣2)
(3)-2<a<2.
【解析】解:(1)①点(2,1)的“关联点”为(2,1);
②如果点A(3,﹣1)的关联点为(3,﹣1);
B(﹣1,3)的“关联点”为(﹣1,﹣3),
一个在函数y=![]() 图象上,那么这个点是 B;
图象上,那么这个点是 B;
所以答案是:(2,1),B;
( 2 )①如果点M*(﹣1,﹣2)是一次函数y=x+3图象上点M的“关联点”是(﹣1,2),
那么点M的坐标为(﹣1,2);②如果点N*(m+1,2)是一次函数y=x+3图象上,
点N*(﹣1,2)的“关联点”(﹣1,﹣2),
点N的坐标是(﹣1,﹣2),
所以答案是:(﹣1,2),(﹣1,﹣2);
( 3 )如果点P在函数y=﹣x2+4(﹣2<x≤a)的图象上,
当﹣2<x≤0时,0<y≤4,即﹣2<a≤0;
当x>0时,y=y′,即﹣4<y≤4,
﹣x2+4>﹣4,解得x<2 ![]() ,
,
即0<x<2 ![]() ,
,
综上所述:﹣2<x<2 ![]() ,
,
﹣2<a<2 ![]() .
.
“关联点”Q的纵坐标y′的取值范围是﹣4<y′≤4,那么实数a的取值范围是﹣2<a<2 ![]() ,
,
所以答案是:﹣2<a<2.
【考点精析】关于本题考查的一次函数的性质和二次函数的图象,需要了解一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】已知:二次函数y=﹣x2+bx+c的图象过点(﹣1,﹣8),(0,﹣3).
(1)求此二次函数的表达式,并用配方法将其化为y=a(x﹣h)2+k的形式;
(2)画出此函数图象的示意图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的奇数1,3,5,7,…排成如图的数表,用如图所示的“十字框”可以框出5个数,这5个数之间将满足一定的关系,按照此方法,若“十字框”框出的5个数的和等于2015,则这5个数中最大数为______.
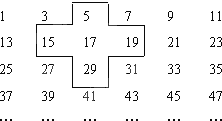
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y1=x2+2x+m﹣5.
(1)如果该二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如果该二次函数的图象与x轴交于A、B两点,与y轴交于点C,且点B的坐标为(1,0),求它的表达式和点C的坐标;
(3)如果一次函数y2=px+q的图象经过点A、C,请根据图象直接写出y2<y1时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2,已知点A,B是数轴上的点,请参照图并思考,完成下列各题.
(1)如果点A表示数-3,将点A向右移动7个单位长度,那么终点B表示的数是_____,A,B两点间的距离是_____;
(2)如果点A表示数3,将A点向左移动7个单位长度,再向右移动5个单位长度,那么终点表示的数是_____,A,B两点间的距离为_____;
(3)如果点A表示数-4,将A点向右移动168个单位长度,再向左移动256个单位长度,那么终点B表示的数是_____,A、B两点间的距离是_____;
(4)一般地,如果A点表示的数为m,将A点向右移动n个单位长度,再向左移动p个单位长度,那么请你猜想终点B表示什么数?A,B两点间的距离为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市实施居民用水阶梯价格制度,按年度用水量计算,将居民家庭全年用水量划分为三个阶梯,水价按阶梯递增:
第一阶梯:年用水量不超过200吨,每吨水价为3元;
第二阶梯:年用水量超过200吨但不超过300吨的部分,每吨水价为3. 5元;
第三阶梯:年用水量超过300吨的部分,每吨水价为6元.
(1)小明家2018年用水180吨,这一年应缴纳水费 元;
(2)小亮家2018年缴纳水费810元,则小亮家这一年用水多少吨?
(3)小红家2017年和2018年共用水600吨,共缴纳水费1950元,并且2018年的用水量超过2017年的用水量,则小红家2017年和2018年各用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2 , 求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求x取何值时,花园面积S最大,并求出花园面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是测量一物体体积的过程:
步骤一:将180 mL的水装进一个容量为300 mL的杯子中;
步骤二:将三个相同的玻璃球放入水中,结果水没有满;
步骤三:再将一个同样的玻璃球放入水中,结果水满溢出.

根据以上过程,推测一个玻璃球的体积在下列哪一范围内?(1 mL=1 cm3)( ).
A. 10 cm3以上,20 cm3以下 B. 20 cm3以上,30 cm3以下
C. 30 cm3以上,40 cm3以下 D. 40 cm3以上,50 cm3以下
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com