Question

【题目】已知二次函数y1=x2+2x+m﹣5．
（1）如果该二次函数的图象与x轴有两个交点，求m的取值范围；
（2）如果该二次函数的图象与x轴交于A、B两点，与y轴交于点C，且点B的坐标为（1，0），求它的表达式和点C的坐标；
（3）如果一次函数y2=px+q的图象经过点A、C，请根据图象直接写出y2＜y1时，x的取值范围．

Answer 1

【答案】
（1）解：∵二次函数y1=x2+2x+m﹣5的图象与x轴有两个交点，

∴△＞0，

∴22﹣4（m﹣5）＞0，

解得：m＜6

（2）解：∵二次函数y1=x2+2x+m﹣5的图象经过点（1，0），

∴1+2+m﹣5=0，

解得：m=2，

∴它的表达式是y1=x2+2x﹣3，

∵当x=0时，y=﹣3，

∴C（0，﹣3）

（3）解：由图象可知：当y2＜y1时，x的取值范围是x＜﹣3或x＞0．

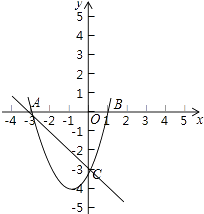
【解析】（1）根据该二次函数的图象与x轴有两个交点可知判别式>0，进而可求出m的范围；
（2）根据该二次函数的图象过点B（1，0），从而求出m的值，可得它的表达式，再由x=0，求得y的值，则可得C的坐标；
（3）根据题意画出图象，再由图象可直接求得.
【考点精析】掌握抛物线与坐标轴的交点是解答本题的根本，需要知道一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．