
【题目】已知![]() 在 数轴上对应的数分别用
在 数轴上对应的数分别用![]() 表示,且
表示,且![]() .
.![]() 是数轴的一动点.
是数轴的一动点.
⑴在数轴上标出![]() 的位置,并求出
的位置,并求出![]() 之间的距离;
之间的距离;
⑵数轴上一点![]() 距
距![]() 点24个单位的长度,其对应的数
点24个单位的长度,其对应的数![]() 满足
满足![]() ,当
,当![]() 点满足
点满足![]() 时,求
时,求![]() 点对应的数.
点对应的数.
⑶动点![]() 从原点开始第一次向左移动1个单位,第二次向右移动3个单位长度,第三次向左移动5个单位长度,第四次向右移动7个单位长度,……点
从原点开始第一次向左移动1个单位,第二次向右移动3个单位长度,第三次向左移动5个单位长度,第四次向右移动7个单位长度,……点![]() 能移动到与
能移动到与![]() 或
或![]() 重合的位置吗?若能,请探究第几次移动时重合;若不能,请说明理由.
重合的位置吗?若能,请探究第几次移动时重合;若不能,请说明理由.
【答案】(1)30;(2)-16或-8;(3)见解析.
【解析】
⑴根据“非负数的和为0,则每一个非负数为0”,可以依次求出![]() 的值,从而使问题解决;⑵.根据
的值,从而使问题解决;⑵.根据![]() ,所以
,所以![]() ;结合⑴问的结论和本问的条件可以求出
;结合⑴问的结论和本问的条件可以求出![]() 的值;
的值;![]() 时,其一,点
时,其一,点![]() 在
在![]() 之间;其二.点
之间;其二.点![]() 在
在![]() 的延长线上.⑶主要是要找移动的规律:主要是找出向右移动的距离规律,从而探究出移动重合的存在性和移动重合的次数.
的延长线上.⑶主要是要找移动的规律:主要是找出向右移动的距离规律,从而探究出移动重合的存在性和移动重合的次数.
⑴. ∵![]() ,且
,且![]()
∴![]() ;解得:
;解得:![]()
∴在数轴上![]() 分别对应的是
分别对应的是![]() 和
和![]() .表示在数轴上:
.表示在数轴上:

∴![]()
⑵. ∵数轴上一点![]() 距
距![]() 点24个单位的长度,可能在左,也可能在右;“右加左减”.
点24个单位的长度,可能在左,也可能在右;“右加左减”.
∴![]() 或
或![]()
∵![]() ∴
∴![]()
又![]() ∴
∴![]() ∴
∴![]()
∴![]()
①.当点![]() 在
在![]() 之间时,
之间时,![]() ;(见下面示意图)
;(见下面示意图)
![]()
∵![]() ∴
∴![]() 解得:
解得:![]()
∴![]() 点对应的数是
点对应的数是![]() ;
;
②. 点![]() 在
在![]() 的延长线上时,
的延长线上时,![]() (见下面示意图)
(见下面示意图)
![]()
∵![]() ∴
∴![]() ,
,![]() .
.
∴![]() 点对应的数是
点对应的数是![]()
③.若点![]() 在
在![]() 的延长线上“
的延长线上“![]() ”不会成立.
”不会成立.
故![]() 点对应的数是
点对应的数是![]() 或
或![]() .
.
⑶.点![]() 能移动到与
能移动到与![]() 重合的位置,不能移动到与
重合的位置,不能移动到与![]() 重合的位置.
重合的位置.
理由如下:
第一次点M表示-1,第二次点P表示2,依次-3,4,-5,6…
则第n次为(-1)nn,
点A表示10,则第10次M与A重合;
点B表示-20,点M与点B不重合.∴点![]() 移动10次与
移动10次与![]() 重合,点M与点B不重合.
重合,点M与点B不重合.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y1=x2+2x+m﹣5.
(1)如果该二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如果该二次函数的图象与x轴交于A、B两点,与y轴交于点C,且点B的坐标为(1,0),求它的表达式和点C的坐标;
(3)如果一次函数y2=px+q的图象经过点A、C,请根据图象直接写出y2<y1时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
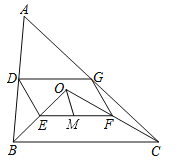
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知直线AB和CD相交于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°.
(1)求∠AON的度数.
(2)写出∠DON的余角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小丽两位同学学习数学都养成了良好的预习习惯.某天他俩预习了课本第107页上的问题3,题目如下:
某小组计划做一批“中国结”,如果每人做5个,那么比计划多了9个;如果每人做4个,那么比计划少15个.该小组共有多少人?计划做多少个“中国结”?
他俩都没有看课本上的解答过程,而是独立思考,分别列出了如下尚不完整的方程:
小明:![]() ; 小丽:
; 小丽:![]() .
.
(1)在小明、小丽所列的方程中,“□”中是运算符号,“( )”中是数字,试分别指出未知数![]() 、
、![]() 表示的意义;
表示的意义;
(2)试选择一种方法,将问题3解答完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是测量一物体体积的过程:
步骤一:将180 mL的水装进一个容量为300 mL的杯子中;
步骤二:将三个相同的玻璃球放入水中,结果水没有满;
步骤三:再将一个同样的玻璃球放入水中,结果水满溢出.

根据以上过程,推测一个玻璃球的体积在下列哪一范围内?(1 mL=1 cm3)( ).
A. 10 cm3以上,20 cm3以下 B. 20 cm3以上,30 cm3以下
C. 30 cm3以上,40 cm3以下 D. 40 cm3以上,50 cm3以下
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O为△ABC的外接圆,直线l与⊙O相切与点P,且l∥BC.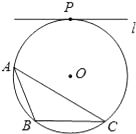
(1)请仅用无刻度的直尺,在⊙O中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法);
(2)请写出证明△ABC被所作弦分成的两部分面积相等的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度.他们采取的方法是:先在地面上的点A处测得杆顶端点P的仰角是45°,再向前走到B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°,这时只需要测出AB的长度就能通过计算求出电线杆PQ的高度.你同意他们的测量方案吗?若同意,画出计算时的图形,简要写出计算的思路,不用求出具体值;若不同意,提出你的测量方案,并简要写出计算思路.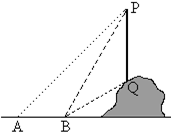
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+10与x轴、y轴分别交于点B,C,点A的坐标为(8,0),P(x,y)是直线y=﹣x+10在第一象限内一个动点.
(1)求△OPA的面积S与x的函数关系式,并写出自变量的x的取值范围;
(2)当△OPA的面积为10时,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com