
【题目】平面内的两条直线有相交和平行两种位置关系.




(1)如图1,若![]() ,点
,点![]() 在
在![]() 外部,则有
外部,则有![]() ,又可证
,又可证![]() ,得
,得![]() ,将点
,将点![]() 移到
移到![]() 内部,如图2,以上结论是否成立?若成立,说明理由;若不成立,则
内部,如图2,以上结论是否成立?若成立,说明理由;若不成立,则![]() 之间有何数量关系?请证明你的结论;
之间有何数量关系?请证明你的结论;
(2)在如图2中,将直线![]() 绕点
绕点![]() 逆时针方向旋转一定角度交直线
逆时针方向旋转一定角度交直线![]() 于点
于点![]() 如图3,则
如图3,则![]()
![]() 之间有何数量关系? (不需证明);
之间有何数量关系? (不需证明);
(3)根据(2)的结论,求如图4中![]() 的度数.
的度数.
【答案】(1)不成立,![]() ;证明见解析;(2)
;证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)延长BP交CD于点E,根据AB∥CD得出∠B=∠BED,再由三角形外角的性质即可得出结论;
(2)连接QP并延长,由三角形外角的性质得出∠BPE=∠B+∠BQE,∠DPE=∠D+∠DQP,由此可得出结论;
(3)由(2)的结论得:∠AFG=∠B+∠E.∠AGF=∠C+∠D.再根据∠A+∠AFG+∠AGF=180°即可得出结论.
解:(1)不成立,结论是∠BPD=∠B+∠D.
延长BP交CD于点E,
∵AB∥CD,
∴∠B=∠BED,
又∵∠BPD=∠BED+∠D,
∴∠BPD=∠B+∠D;

(2)结论:∠BPD=∠BQD+∠B+∠D.
连接QP并延长,
∵∠BPE是△BPQ的外角,∠DPE是△PDQ的外角,
∴∠BPE=∠B+∠BQE,∠DPE=∠D+∠DQP,
∴∠BPE+∠DPE=∠B+∠D+∠BQE+∠DQP,
即∠BPD=∠BQD+∠B+∠D;

(3)由(2)的结论得:∠AFG=∠B+∠E.∠AGF=∠C+∠D.
又∵∠A+∠AFG+∠AGF=180°
∴∠A+∠B+∠C+∠D+∠E=180°.


科目:初中数学 来源: 题型:
【题目】已知E、F分别为正方形ABCD的边BC、CD上的点,且∠EAF=45°.
(1)如图①求证:BE+DF=EF;
(2)连接BD分别交AE、AF于M、N,
①如图②,若AB=6![]() ,BM=3,求MN.
,BM=3,求MN.
②如图③,若EF∥BD,求证:MN=CE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据所学知识完成小题:
(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等边△ABE和等边△ACD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.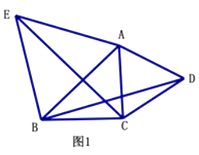
(2)【深入探究】如图2,△ABC中,∠ABC=45°,AB=5cm,BC=3cm,分别以AB、AC为边向外作正方形ABNE和正方形ACMD,连接BD,求BD的长.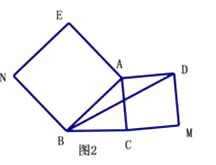
(3)如图3,在(2)的条件下,以AC为直角边在线段AC的左侧作等腰直角△ACD,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=6,OB=8,OC=10,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为8;③S四边形AOBO′=24+12![]() ;④S△AOC+S△AOB=24+9
;④S△AOC+S△AOB=24+9![]() ;⑤S△ABC=36+25
;⑤S△ABC=36+25![]() ; 其中正确的结论有( )
; 其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com