
ЁОЬтФПЁПГЩЖМЪаЕФЫЎЗбЪЕааЯТБэЕФЪеЗбЗНЪНЃК
УПдТгУЫЎСП | ЕЅМл |
ВЛГЌГі | 2дЊ/ |
ГЌГі | 3дЊ/ |
ГЌГі | 4дЊ/ |
ЃЈ1ЃЉжмРЯЪІМвОХдТЗнгУСЫ![]() ЕФЫЎЃЌгІИЖЖрЩйЫЎЗбЃП
ЕФЫЎЃЌгІИЖЖрЩйЫЎЗбЃП
ЃЈ2ЃЉШчЙћРюРЯЪІМвОХдТЗнЕФгУЫЎСПЮЊ![]() ЃЌФЧУДгІИЖЕФЫЎЗбЮЊЖрЩйдЊЃП
ЃЌФЧУДгІИЖЕФЫЎЗбЮЊЖрЩйдЊЃП
ЃЈ3ЃЉШчЙћВмРЯЪІМвОХдТКЭЪЎдТвЛЙВгУСЫ![]() ЕФЫЎЃЌЧввбжЊОХдТБШЪЎдТЩйЃЌЩшОХдТгУЫЎСПЮЊ
ЕФЫЎЃЌЧввбжЊОХдТБШЪЎдТЩйЃЌЩшОХдТгУЫЎСПЮЊ![]() ЃЌФЧУДВмРЯЪІетСНИідТвЛЙВвЊНЛЖрЩйЧЎЕФЫЎЗбЃПЃЈПЩгУКЌ
ЃЌФЧУДВмРЯЪІетСНИідТвЛЙВвЊНЛЖрЩйЧЎЕФЫЎЗбЃПЃЈПЩгУКЌ![]() ЕФДњЪ§ЪНБэЪОЃЉ
ЕФДњЪ§ЪНБэЪОЃЉ
ЁОД№АИЁПЃЈ1ЃЉ38дЊЃЛЃЈ2ЃЉЕБ![]() ЪБЃЌгІИЖЫЎЗб10xдЊЃЛЕБ
ЪБЃЌгІИЖЫЎЗб10xдЊЃЛЕБ![]() ЪБЃЌгІИЖЫЎЗб
ЪБЃЌгІИЖЫЎЗб![]() ЃЈдЊЃЉЃЛЕБ
ЃЈдЊЃЉЃЛЕБ![]() ЪБЃЌгІИЖЫЎЗбЮЊ
ЪБЃЌгІИЖЫЎЗбЮЊ![]() ЃЈдЊЃЉЃЛЃЈ3ЃЉШє
ЃЈдЊЃЉЃЛЃЈ3ЃЉШє![]() ЃЌвЊНЛЫЎЗб
ЃЌвЊНЛЫЎЗб![]() ЃЈдЊЃЉЃЛШє
ЃЈдЊЃЉЃЛШє![]() ЃЌвЊНЛЫЎЗбЮЊ
ЃЌвЊНЛЫЎЗбЮЊ![]() ЃЈдЊЃЉЃЛШє
ЃЈдЊЃЉЃЛШє![]() ЃЌвЊНЛЫЎЗбЮЊ
ЃЌвЊНЛЫЎЗбЮЊ![]() дЊЃЎ
дЊЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнВЛГЌ![]() ЕФАДее2дЊ/
ЕФАДее2дЊ/![]() МЦЫуЃЌГЌГі
МЦЫуЃЌГЌГі![]() ЕФ6
ЕФ6![]() АДее3дЊ/
АДее3дЊ/![]() МЦЫуЃЌОнДЫНтД№МДПЩЃЛ
МЦЫуЃЌОнДЫНтД№МДПЩЃЛ
ЃЈ2ЃЉЗжгУЫЎСПВЛГЌГі![]() ЃЈАќРЈ
ЃЈАќРЈ![]() ЃЉЁЂГЌГі
ЃЉЁЂГЌГі![]() ЕЋВЛГЌГі
ЕЋВЛГЌГі![]() ЃЈАќРЈ
ЃЈАќРЈ![]() ЃЉЁЂГЌГі
ЃЉЁЂГЌГі![]() Ш§жжЧщПіЃЌАДеегІИЖЫЎЗбЕФМЦЫуЗНЗЈНтД№МДПЩЃЛ
Ш§жжЧщПіЃЌАДеегІИЖЫЎЗбЕФМЦЫуЗНЗЈНтД№МДПЩЃЛ
ЃЈ3ЃЉЯШИљОнОХдТБШЪЎдТгУЫЎСПЩйШЗЖЈxЕФЗЖЮЇЪЧ![]() ЃЌШЛКѓЗж
ЃЌШЛКѓЗж![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§жжЧщПіЃЌдйИљОнЃЈ2ЃЉЬтжаЕФНсТлКЭМЦЗбЗНЗЈНтД№МДПЩЃЎ
Ш§жжЧщПіЃЌдйИљОнЃЈ2ЃЉЬтжаЕФНсТлКЭМЦЗбЗНЗЈНтД№МДПЩЃЎ
НтЃКЃЈ1ЃЉ![]() дЊЃЌ
дЊЃЌ
Д№ЃКжмРЯЪІМвОХдТЗнгІИЖЫЎЗб38дЊЃЛ
ЃЈ2ЃЉЕБгУЫЎСПВЛГЌГі![]() ЃЈАќРЈ
ЃЈАќРЈ![]() ЃЉМД
ЃЉМД![]() ЪБЃЌгІИЖЫЎЗбЮЊ10xдЊЃЛ
ЪБЃЌгІИЖЫЎЗбЮЊ10xдЊЃЛ
ЕБгУЫЎСПГЌГі![]() ЕЋВЛГЌГі
ЕЋВЛГЌГі![]() ЃЈАќРЈ
ЃЈАќРЈ![]() ЃЉМД
ЃЉМД![]() ЪБЃЌгІИЖЫЎЗбЮЊ
ЪБЃЌгІИЖЫЎЗбЮЊ![]() ЃЈдЊЃЉЃЛ
ЃЈдЊЃЉЃЛ
ЕБгУЫЎСПГЌГі![]() МД
МД![]() ЪБЃЌгІИЖЫЎЗбЮЊ
ЪБЃЌгІИЖЫЎЗбЮЊ![]() ЃЈдЊЃЉЃЛ
ЃЈдЊЃЉЃЛ
Д№ЃКЕБ![]() ЪБЃЌгІИЖЫЎЗб10xдЊЃЛЕБ
ЪБЃЌгІИЖЫЎЗб10xдЊЃЛЕБ![]() ЪБЃЌгІИЖЫЎЗб
ЪБЃЌгІИЖЫЎЗб![]() ЃЈдЊЃЉЃЛЕБ
ЃЈдЊЃЉЃЛЕБ![]() ЪБЃЌгІИЖЫЎЗбЮЊ
ЪБЃЌгІИЖЫЎЗбЮЊ![]() ЃЈдЊЃЉЃЛ
ЃЈдЊЃЉЃЛ
ЃЈ3ЃЉвђЮЊОХдТБШЪЎдТгУЫЎСПЩйЃЌЫљвд![]() ЃЌ
ЃЌ
Шє![]() ЃЌдђ
ЃЌдђ![]() ЃЌЫљвдВмРЯЪІетСНИідТвЛЙВвЊНЛЫЎЗбЮЊ
ЃЌЫљвдВмРЯЪІетСНИідТвЛЙВвЊНЛЫЎЗбЮЊ![]() ЃЈдЊЃЉЃЛ
ЃЈдЊЃЉЃЛ
Шє![]() ЃЌдђ
ЃЌдђ![]() ЃЌЫљвдВмРЯЪІетСНИідТвЛЙВвЊНЛЫЎЗбЮЊ
ЃЌЫљвдВмРЯЪІетСНИідТвЛЙВвЊНЛЫЎЗбЮЊ![]() ЃЈдЊЃЉЃЛ
ЃЈдЊЃЉЃЛ
Шє![]() ЃЌдђ
ЃЌдђ![]() ЃЌЫљвдВмРЯЪІетСНИідТвЛЙВвЊНЛЫЎЗбЮЊ
ЃЌЫљвдВмРЯЪІетСНИідТвЛЙВвЊНЛЫЎЗбЮЊ![]() дЊЃЎ
дЊЃЎ
Д№ЃКШє![]() ЃЌвЊНЛЫЎЗб
ЃЌвЊНЛЫЎЗб![]() ЃЈдЊЃЉЃЛШє
ЃЈдЊЃЉЃЛШє![]() ЃЌвЊНЛЫЎЗбЮЊ
ЃЌвЊНЛЫЎЗбЮЊ![]() ЃЈдЊЃЉЃЛШє
ЃЈдЊЃЉЃЛШє![]() ЃЌвЊНЛЫЎЗбЮЊ
ЃЌвЊНЛЫЎЗбЮЊ![]() дЊЃЎ
дЊЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
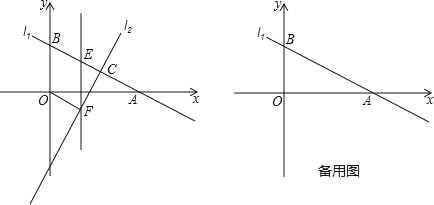
ЁОЬтФПЁПШчЭМЃЌжБЯп![]() ЗжБ№гыxжсЁЂyжсНЛгк
ЗжБ№гыxжсЁЂyжсНЛгк![]() СНЕуЃЌгыжБЯп
СНЕуЃЌгыжБЯп![]() НЛгкЕуCЃЈ4ЃЌ2ЃЉЃЎ
НЛгкЕуCЃЈ4ЃЌ2ЃЉЃЎ
ЃЈ1ЃЉЕуAзјБъЮЊЃЈ ЃЌ ЃЉЃЌBЮЊЃЈ ЃЌ ЃЉЃЛ
ЃЈ2ЃЉдкЯпЖЮ![]() ЩЯгавЛЕуEЃЌЙ§ЕуEзїyжсЕФЦНааЯпНЛжБЯп
ЩЯгавЛЕуEЃЌЙ§ЕуEзїyжсЕФЦНааЯпНЛжБЯп![]() гкЕуFЃЌЩшЕуEЕФКсзјБъЮЊmЃЌЕБmЮЊКЮжЕЪБЃЌЫФБпаЮ
гкЕуFЃЌЩшЕуEЕФКсзјБъЮЊmЃЌЕБmЮЊКЮжЕЪБЃЌЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃЛ
ЪЧЦНааЫФБпаЮЃЛ
ЃЈ3ЃЉШєЕуPЮЊxжсЩЯвЛЕуЃЌдђдкЦНУцжБНЧзјБъЯЕжаЪЧЗёДцдквЛЕуQЃЌЪЙЕУ![]() ЫФИіЕуФмЙЙГЩвЛИіСтаЮЃЎШєДцдкЃЌЧѓГіЫљгаЗћКЯЬѕМўЕФQЕузјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЫФИіЕуФмЙЙГЩвЛИіСтаЮЃЎШєДцдкЃЌЧѓГіЫљгаЗћКЯЬѕМўЕФQЕузјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЙигкxЁЂyЕФЖўдЊвЛДЮЗНГЬзщ ![]() ЕФНтТњзуx+yЃО1ЃЌдђЪЕЪ§kЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
ЕФНтТњзуx+yЃО1ЃЌдђЪЕЪ§kЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
A.kЃМ0
B.kЃМЉ1
C.kЃМЉ2
D.kЃМЉ3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
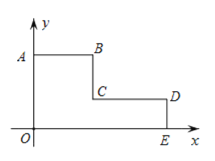
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуOЃЌAЃЌBЃЌCЃЌDЃЌEЕФзјБъЗжБ№ЮЊЃЈ0ЃЌ0ЃЉЃЈ0ЃЌ5ЃЉЃЌЃЈ4ЃЌ5ЃЉЃЌЃЈ4ЃЌ2ЃЉЃЌЃЈ9ЃЌ2ЃЉЃЌЃЈ9ЃЌ0ЃЉЃЎ
ЃЈ1ЃЉЧѓетИіЭМаЮЕФжмГЄЃЛ
ЃЈ2ЃЉЧѓетИіЭМаЮЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЄГЇЖдСуМўНјааМьВтЃЌв§НјСЫМьВтЛњЦїЃЎвбжЊвЛЬЈМьВтЛњЕФЙЄзїаЇТЪЯрЕБгквЛУћМьВтдБЕФ20БЖЃЎШєгУетЬЈМьВтЛњМьВт900ИіСуМўвЊБШ15УћМьВтдБМьВтетаЉСуМўЩй3аЁЪБЃЎ
ЃЈ1ЃЉЧѓвЛЬЈСуМўМьВтЛњУПаЁЪБМьВтСуМўЖрЩйИіЃП
ЃЈ2ЃЉЯжгавЛЯюСуМўМьВтШЮЮёЃЌвЊЧѓВЛГЌЙ§7аЁЪБМьВтЭъГЩ3450ИіСуМўЃЎИУГЇЕїХфСЫ2ЬЈМьВтЛњКЭ30УћМьВтдБЃЌЙЄзї3аЁЪБКѓгжЕїХфСЫвЛаЉМьВтЛњНјаажЇдЎЃЌдђИУГЇжСЩйдйЕїХфМИЬЈМьВтЛњВХФмЭъГЩШЮЮёЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌ![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЩЯвЛЕуЃЌ
ЩЯвЛЕуЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШє![]() ЃЌдђ
ЃЌдђ![]() ЁЁ ЁЁЁуЃЛ
ЁЁ ЁЁЁуЃЛ
ЃЈ2ЃЉШєЕу![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌЧѓжЄЃК
ЕФжаЕуЃЌЧѓжЄЃК![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
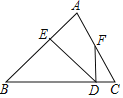
ЁОЬтФПЁПвбжЊЁїABCЮЊБпГЄЮЊ6ЕФЕШБпШ§НЧаЮЃЌDЃЌEЗжБ№дкБпBCЃЌACЩЯЃЌЧвCD=CE=xЃЌСЌНгDEВЂбгГЄжСЕуFЃЌЪЙEF=AEЃЌСЌНгAFЃЌCFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїAEFЮЊЕШБпШ§НЧаЮЃЛ
ЃЈ2ЃЉЧѓжЄЃКЫФБпаЮABDFЪЧЦНааЫФБпаЮЃЛ
ЃЈ3ЃЉМЧЁїCEFЕФУцЛ§ЮЊSЃЌ
ЂйЧѓSгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЂкЕБSгазюДѓжЕЪБЃЌХаЖЯCFгыBCЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЪ§жсЩЯЕуAБэЪОЕФЪ§ЮЊ8ЃЌBЪЧЪ§жсЩЯвЛЕуЃЌЧвAB=14ЃЎЖЏЕуPДгЕуAГіЗЂЃЌвдУПУы5ИіЕЅЮЛГЄЖШЕФЫйЖШбиЪ§жсЯђзѓдШЫйдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtЃЈtЃО0ЃЉУыЃЎ
![]()
ЃЈ1ЃЉаДГіЪ§жсЩЯЕуBБэЪОЕФЪ§ ЃЌЕуPБэЪОЕФЪ§ ЃЈгУКЌtЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ2ЃЉЖЏЕуQДгЕуBГіЗЂЃЌвдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШбиЪ§жсЯђзѓдШЫйдЫЖЏЃЌШєЕуPЁЂQЭЌЪБГіЗЂЃЌЮЪЕуPдЫЖЏЖрЩйУыЪБзЗЩЯЕуQЃП
ЃЈ3ЃЉШєMЮЊAPЕФжаЕуЃЌNЮЊPBЕФжаЕуЃЎЕуPдкдЫЖЏЕФЙ§ГЬжаЃЌЯпЖЮMNЕФГЄЖШЪЧЗёЗЂЩњБфЛЏЃПШєБфЛЏЃЌЧыЫЕУїРэгЩЃЛШєВЛБфЃЌЧыФуЛГіЭМаЮЃЌВЂЧѓГіЯпЖЮMNЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
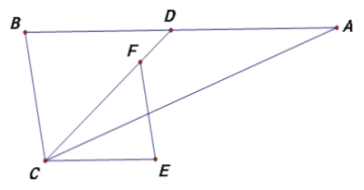
ЁОЬтФПЁПШчЭМ,дкШ§НЧаЮ![]() жа,
жа, ![]() ,Еу
,Еу![]() ЪЧ
ЪЧ![]() ЩЯвЛЕу,Еу
ЩЯвЛЕу,Еу![]() ЪЧШ§НЧаЮЭтЩЯвЛЕу, Чв
ЪЧШ§НЧаЮЭтЩЯвЛЕу, Чв![]() Еу
Еу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЩЯвЛЕуЃЌСЌНг
ЩЯвЛЕуЃЌСЌНг![]() ЃЌЧв
ЃЌЧв![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§
ЕФЖШЪ§
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com