解:(1)原式=9a
4b
6×(-a
15b
10)=-9
19b
16;
(2)原式=-7×
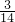
×

×x
2+3+1y
2+1+4=-x
6y
7;
(3)原式=-6a
2+1b
2-3a
2b
2+3ab=-6a
3b
2-3a
3b
2+3ab;
(4)原式=-12a
1+2b
3+1-4a
1+2b
2+1+6a
1+2b
1+1-2a
2b=-12a
3b
4-4a
3b
3+6a
3b
2-2a
2b;
(5)原式=x
3-2x
2-3x+x
2y-2xy-3y;
(6)原式=3a
nb
2+n-1-2a
n+2b
2+n+1-a
nb
2=3a
nb
n+1-2a
n+1b
n+3-a
nb
2;
(7)原式=8x
2+6y
3+2x
2+1y
4-2x
2=8x
8y
3+2x
3y
4-2x
2;
(8)原式=9x
2-y
2-16x
2+9y
2=-7x
2+8y
2.
分析:本题可用整式的运算的一般规则进行计算即可.同底数幂相乘除时底数不变,指数相加减.积的乘方是先把积中的每一个乘数分别乘方,再把所得的幂相乘.
点评:本题考查了整式的混合运算,要注意计算过程中熟练掌握因式分解的应用,同底数幂的乘除运算法则等.

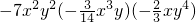 ;
;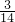 ×
× ×x2+3+1y2+1+4=-x6y7;
×x2+3+1y2+1+4=-x6y7;
