
 ��
�� �ȣ�ͼ2�������е����������Ƿ���Ȼ��������������ѡ������һ������֤����������������˵�����ɡ�
�ȣ�ͼ2�������е����������Ƿ���Ȼ��������������ѡ������һ������֤����������������˵�����ɡ�

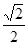 a��FK=
a��FK=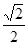 b��
b��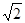 b
b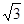 ��1
��1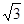 ��ʱ��AFH����Ϊ�������Ρ�
��ʱ��AFH����Ϊ�������Ρ�


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ͬ����
ͬ���� ������ׯ��
������ׯ�� ��
��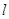 �ľ���ֱ���3km��2km��
�ľ���ֱ���3km��2km��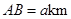
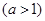 ���ּƻ��ںӰ�
���ּƻ��ںӰ�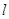 �Ͻ�һ��ˮվ
�Ͻ�һ��ˮվ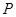 ������ˮ����������ׯ��ˮ��
������ˮ����������ׯ��ˮ��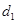 ����
����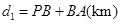 ������
������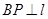 �ڵ�
�ڵ�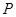 ����ͼ��2���Ƿ�������ʾ��ͼ����÷����йܵ�����Ϊ
����ͼ��2���Ƿ�������ʾ��ͼ����÷����йܵ�����Ϊ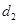 ����
����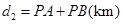 �����е�
�����е�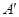 ���
���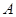 ����
����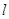 �Գƣ�
�Գƣ� ��
��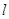 ���ڵ�
���ڵ�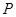 ����
����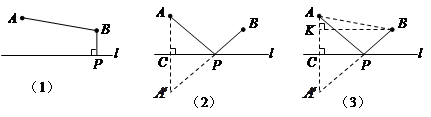
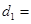 km���ú�
km���ú� ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����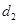 �ij���������ͼ��3����ʾ�ĸ����ߣ����㰴С��ͬѧ��˼·���㣬
�ij���������ͼ��3����ʾ�ĸ����ߣ����㰴С��ͬѧ��˼·���㣬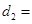 km���ú�
km���ú� ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����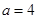 ʱ���Ƚϴ�С��
ʱ���Ƚϴ�С�� �����������������������
�����������������������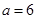 ʱ���Ƚϴ�С��
ʱ���Ƚϴ�С�� �����������������������
����������������������� ����
����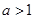 ʱ��������ȡֵ������з�����Ҫʹ����Ĺܵ����Ƚ϶̣�Ӧѡ��һ���Ƿ�������
ʱ��������ȡֵ������з�����Ҫʹ����Ĺܵ����Ƚ϶̣�Ӧѡ��һ���Ƿ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A��ֱ�������� | B��������� | C�������� | D���������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| �� | A�� | ��0����2�� | B�� | ��0��0�� | C�� | ����2��0�� | D�� | ��0��4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com