
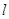 同侧有
同侧有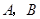 两个村庄,
两个村庄,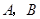 到
到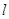 的距离分别是3km和2km,
的距离分别是3km和2km,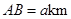
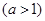 .现计划在河岸
.现计划在河岸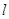 上建一抽水站
上建一抽水站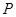 ,用输水管向两个村庄供水.
,用输水管向两个村庄供水.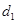 ,且
,且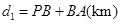 (其中
(其中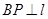 于点
于点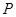 );图(2)是方案二的示意图,设该方案中管道长度为
);图(2)是方案二的示意图,设该方案中管道长度为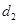 ,且
,且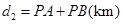 (其中点
(其中点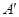 与点
与点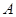 关于
关于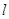 对称,
对称, 与
与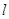 交于点
交于点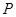 ).
).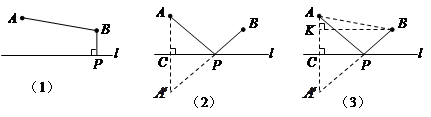
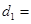 km(用含
km(用含 的式子表示);
的式子表示);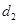 的长,作了如图(3)所示的辅助线,请你按小宇同学的思路计算,
的长,作了如图(3)所示的辅助线,请你按小宇同学的思路计算,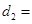 km(用含
km(用含 的式子表示).
的式子表示).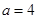 时,比较大小:
时,比较大小: (填“>”、“=”或“<”);
(填“>”、“=”或“<”);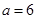 时,比较大小:
时,比较大小: (填“>”、“=”或“<”);
(填“>”、“=”或“<”); (当
(当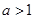 时)的所有取值情况进行分析,要使铺设的管道长度较短,应选择方案一还是方案二?
时)的所有取值情况进行分析,要使铺设的管道长度较短,应选择方案一还是方案二?
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.110° | B.80° | C.90° | D.100° |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 在正方形网格中,若点
在正方形网格中,若点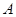 的坐标为
的坐标为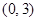 ,按要求回答下列问题:
,按要求回答下列问题: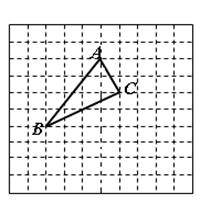
 和点
和点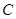 的坐标;
的坐标; 关于
关于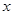 轴的对称图形
轴的对称图形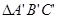 (不用写作法),并写出
(不用写作法),并写出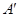 、
、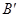 、
、 的坐标.
的坐标.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
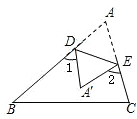
| A.∠A=∠1+∠2 | B.∠A=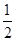 (∠1+∠2) (∠1+∠2) | C.∠A= 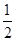 (∠2-∠1) (∠2-∠1) | D.∠A= ∠2-∠1 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 。
。 度(图2),⑴中的两个结论是否仍然成立?若成立,选择其中一个加以证明,若不成立,请说明理由。
度(图2),⑴中的两个结论是否仍然成立?若成立,选择其中一个加以证明,若不成立,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com