
【题目】如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,若MA=MC. 
(1)求证:CD=AN;
(2)若AC⊥DN,∠CAN=30°,MN=1,求四边形ADCN的面积.
【答案】
(1)证明:
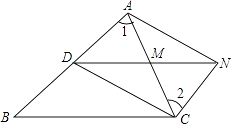
∵CN∥AB,
∴∠1=∠2.
在△AMD和△CMN中,
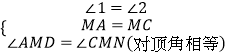 ,
,
∴△AMD≌△CMN(ASA),
∴AD=CN.
又AD∥CN,
∴四边形ADCN是平行四边形,
∴CD=AN;
(2)解:∵AC⊥DN,∠CAN=30°,MN=1,
∴AN=2MN=2,
∴AM= ![]() =
= ![]() ,
,
∴S△AMN= ![]() AMMN=
AMMN= ![]() ×
× ![]() ×1=
×1= ![]() .
.
∵四边形ADCN是平行四边形,
∴S四边形ADCN=4S△AMN=2 ![]() .
.
【解析】(1)利用“平行四边形ADCN的对边相等”的性质可以证得CD=AN;(2)根据“直角△AMN中的30度角所对的直角边是斜边的一半”求得AN=2MN=2,然后由勾股定理得到AM= ![]() ,则S四边形ADCN=4S△AMN=2
,则S四边形ADCN=4S△AMN=2 ![]() .
.
【考点精析】根据题目的已知条件,利用勾股定理的概念和平行四边形的判定与性质的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
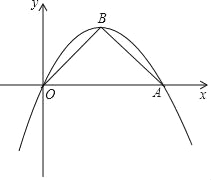
【题目】如图,在平面直角坐标系xOy,已知二次函数y=﹣![]() x2+bx的图象过点A(4,0),顶点为B,连接AB、BO.
x2+bx的图象过点A(4,0),顶点为B,连接AB、BO.
(1)求二次函数的表达式;
(2)若C是BO的中点,点Q在线段AB上,设点B关于直线CQ的对称点为B',当△OCB'为等边三角形时,求BQ的长度;
(3)若点D在线段BO上,OD=2DB,点E、F在△OAB的边上,且满足△DOF与△DEF全等,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间 (小时) | 2 | 2.5 | 3 | 3.5 | 4 |
学生人数(名) | 1 | 2 | 8 | 6 | 3 |
则关于这20名学生阅读小时数的说法正确的是( )
A. 众数是8 B. 中位数是3 C. 平均数是3 D. 方差是0.34
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三军受命,我解放军各部队奋力抗战地救灾一线.现有甲、乙两支解放军小分队将救灾物资送往某重灾小镇,甲队先出发,从部队基地到小镇只有唯一通道,且路程为24km,如图是他们行走的路线关于时间的函数图象,四位同学观察此函数图象得出有关信息,其中正确的个数是( ) 
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小康放学回家后,问爸爸、妈妈火箭队与太阳队篮球比赛的结果,爸爸说:“本场比赛太阳队的奥尼尔比火箭队的姚明多得了12分”,妈妈说:“姚明得分的两倍与奥尼尔得分的差大于10;奥尼尔得分的两倍比姚明得分的3倍还多”,爸爸又说:“姚明得分超过20分,则火箭队赢,否则太阳队赢”。请你帮小康分析一下,究竟是哪个队赢了,本场比赛姚明、奥尼尔各得了多少分?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com