
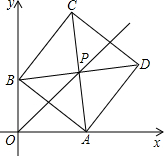
 在平面直角坐标系xOy中,边长为2的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C,D都在第一象限.
在平面直角坐标系xOy中,边长为2的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C,D都在第一象限.分析 (1)证明四边形AOBP是正方形,根据边长为2的正方形ABCD求OA的长,写出点P的坐标;
(2)作辅助线,根据角平分线性质定理的逆定理,只要再证明PG=PH即可,根据证明△PGB≌△PHA,可以得出结论;
(3)当点B与O重合时,如图3,n最小,当BD∥x轴时,如图1,此时点P到x轴的距离为PA,此时n最大,分别求出即可.
解答 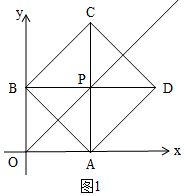 解:(1)如图1,∵∠AOB=90°,∠BAO=45°,
解:(1)如图1,∵∠AOB=90°,∠BAO=45°,
∴△AOB是等腰直角三角形,
∴OB=OA,
∵四边形ABCD为正方形,
∴∠BAP=45°,AC⊥BD,
∴∠OAP=45°+45°=90°,∠APB=90°,
∴∠AOB=∠OAP=∠APB=90°,
∴四边形AOBP是矩形,
∵OB=OA,
∴矩形AOBP为正方形,
∵AB=2,
∴OA=AP=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,
∴P($\sqrt{2}$,$\sqrt{2}$);
(2)如图2,过P作PG⊥y轴于G,PH⊥x轴于H,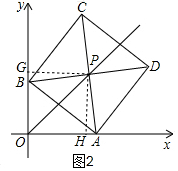
∵∠PGO=∠GOH=∠OHP=90°,
∴∠GPH=90°,
∴∠GPB+∠BPH=90°,
∵∠APB=90°,
∴∠BPH+∠APH=90°,
∴∠GPB=∠APH,
∵四边形ABCD为正方形,
∴PB=PA,
∵∠PGB=∠PHA=90°,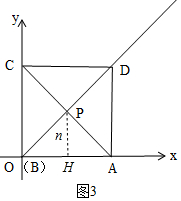
∴△PGB≌△PHA,
∴PG=PH,
∴点P都在∠AOB的平分线上,
即无论点A在x轴正半轴上、点B在y轴正半轴上怎样运动,点P都在∠AOB的平分线上;
(3)当点B与O重合时,如图3,
△ABP是等腰直角三角形,
∴PH=$\frac{1}{2}$AB=1,
∴此时n=1,
当BD∥x轴时,如图1,此时点P到x轴的距离为PA,即n=PA=$\sqrt{2}$,
∴1<n≤$\sqrt{2}$.
点评 本题是四边形的综合题,考查了正方形的性质、矩形的性质和判定、等腰直角三角形、三角形全等的性质和判定,熟练掌握正方形和等腰直角三角形的性质是关键,注意图形与坐标特点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
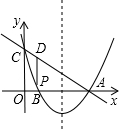 如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从点C沿抛物线向A点运动(运动到A点停止),过点P作PD∥y轴交直线AC于点D.
如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从点C沿抛物线向A点运动(运动到A点停止),过点P作PD∥y轴交直线AC于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
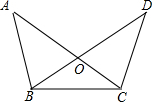 如图,在△OBC中,延长BO到D,延长CO到A,要证明OD=OA,则应添加条件中错误的是( )
如图,在△OBC中,延长BO到D,延长CO到A,要证明OD=OA,则应添加条件中错误的是( )| A. | △ABC≌△DCB | B. | OB=OC,∠A=∠D | C. | OB=OC,AB=DC | D. | ∠A=∠D,∠ABC=∠DCB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com