
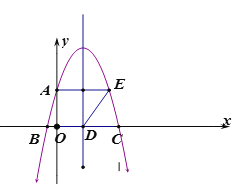
【题目】已知:如图抛物线y=ax2+bx+![]() 与y轴交于点A,与x轴交于点B、点C.连接AB,以AB为边向右作平行四边形ABDE,点E落在抛物线上,点D落在x轴上,若抛物线的对称轴恰好经过点D,且∠ABD=60°,则这条抛物线的解析式为( )
与y轴交于点A,与x轴交于点B、点C.连接AB,以AB为边向右作平行四边形ABDE,点E落在抛物线上,点D落在x轴上,若抛物线的对称轴恰好经过点D,且∠ABD=60°,则这条抛物线的解析式为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
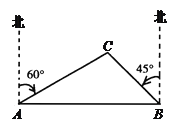
【题目】已知:如图,一艘渔船正在港口A的正东方向40海里的B处进行捕鱼作业,突然接到通知,要该船前往C岛运送一批物资到A港,已知C岛在A港的北偏东60°方向,且在B的北偏西45°方向.问该船从B处出发,以平均每小时20海里的速度行驶,需要多少时间才能把这批物资送到A港(精确到1小时)(该船在C岛停留半个小时)?(![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
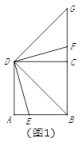
【题目】⑴如图1,![]() 是正方形
是正方形![]() 边
边![]() 上的一点,连接
上的一点,连接![]() ,将
,将![]() 绕着点
绕着点![]() 逆时针旋转90°,旋转后角的两边分别与射线
逆时针旋转90°,旋转后角的两边分别与射线![]() 交于点
交于点![]() 和点
和点![]() .
.
①线段![]() 和
和![]() 的数量关系是 ;
的数量关系是 ;
②写出线段![]() 和
和![]() 之间的数量关系.
之间的数量关系.
⑵当四边形![]() 为菱形,
为菱形,![]() ,点
,点![]() 是菱形
是菱形![]() 边
边![]() 所在直线上的一点,连接
所在直线上的一点,连接![]() ,将
,将![]() 绕着点
绕着点![]() 逆时针旋转120°,旋转后角的两边分别与射线
逆时针旋转120°,旋转后角的两边分别与射线![]() 交于点
交于点![]() 和点
和点![]() .
.
①如图2,点![]() 在线段上时,请探究线段
在线段上时,请探究线段![]() 和
和![]() 之间的数量关系,写出结论并给出证明;
之间的数量关系,写出结论并给出证明;
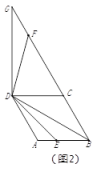
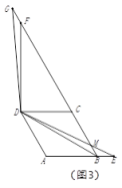
②如图3,点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() 交射线
交射线![]() 于点
于点![]() ;若
;若 ![]() ,直接写出线段
,直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
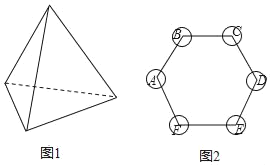
【题目】图①是一枚质地均匀的正四面体形状的骰子,每个面上分别标有数字2,3,4,5.图②是一个正六边形棋盘,现通过掷骰子的方式玩跳棋游戏,规则是:将这枚骰子在桌面掷出后,看骰子落在桌面上(即底面)的数字是几,就从图中的A点开始沿着顺时针方向连续跳动几个顶点,第二次从第一次的终点处开始,按第一次的方法继续……
(1)随机掷一次骰子,则棋子跳动到点C处的概率是 .
(2)随机掷两次骰子,用画树状图或列表的方法,求棋子最终跳动到点C处的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”假期,成都某公司组织部分员工分别到甲、乙、丙、丁四地考察,公司按定额购买了前往各地的车票,如图是用来制作完整的车票种类和相应数量的条形统计图,根据统计图回答下列问题:
![]() 若去丙地的车票占全部车票的
若去丙地的车票占全部车票的![]() ,则总票数为______ 张,去丁地的车票有______ 张
,则总票数为______ 张,去丁地的车票有______ 张![]()
![]() 若公司采用随机抽取的方式发车票,小胡先从所有的车票中随机抽取一张
若公司采用随机抽取的方式发车票,小胡先从所有的车票中随机抽取一张![]() 所有车票的形状、大小、质地完全相同、均匀
所有车票的形状、大小、质地完全相同、均匀![]() ,那么员工小胡抽到去甲地的车票的概率是多少?
,那么员工小胡抽到去甲地的车票的概率是多少?
![]() 若有一张车票,小王和小李都想要,他们决定采取掷一枚质地均匀的正方体骰子的方式来确定给谁,其上的数字是3的倍数,则给小王,否则给小李
若有一张车票,小王和小李都想要,他们决定采取掷一枚质地均匀的正方体骰子的方式来确定给谁,其上的数字是3的倍数,则给小王,否则给小李![]() 请问这个规则对双方是否公平?若公平请说明理由;若不公平,请通过计算说明对谁更有利.
请问这个规则对双方是否公平?若公平请说明理由;若不公平,请通过计算说明对谁更有利.

查看答案和解析>>
科目:初中数学 来源: 题型:
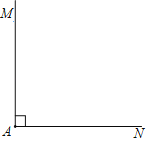
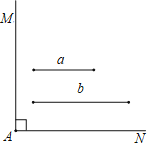
【题目】已知:如图,∠MAN=90°,线段a和线段b
求作:矩形ABCD,使得矩形ABCD的两条边长分别等于线段a和线段b.
下面是小东设计的尺规作图过程.
作法:如图,
①以点A为圆心,b为半径作弧,交AN于点B;
②以点A为圆心,a为半径作弧,交AM于点D;
③分别以点B、点D为圆心,a、b长为半径作弧,两弧交于∠MAN内部的点C;
④分别连接BC,DC.
所以四边形ABCD就是所求作的矩形.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:
∵AB= ;AD= ;
∴四边形ABCD是平行四边形.
∵∠MAN=90°;
∴四边形ABCD是矩形( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点O、D分别为AB、BC的中点,做⊙O与AC相切于点E,在AC边上取一点F,使DF=DO.
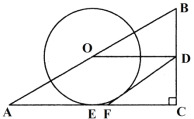
⑴求证:DF是⊙O切线;⑵若sinB=![]() ,CF=2,求⊙O的半径.
,CF=2,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com