
 ,求出点P的坐标.
,求出点P的坐标. ∠MNB,ES⊥x轴于S,当M点运动时,问的
∠MNB,ES⊥x轴于S,当M点运动时,问的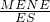 值是否发生变化?若不变,求其值;若变化,请说明理由.
值是否发生变化?若不变,求其值;若变化,请说明理由.
 AB(OC+OF)=
AB(OC+OF)= AB(4+1)=15,
AB(4+1)=15,
 x2+x+4.
x2+x+4.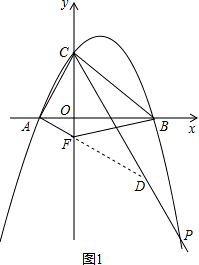 (2)在△ACF中,OA=2、OF=1、OC=4,即:
(2)在△ACF中,OA=2、OF=1、OC=4,即: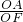 =
=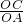 ,
, =2
=2 ,tan∠DCA=
,tan∠DCA= ,则:AD=3
,则:AD=3 ;
;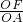 =
= ,
, ,cos∠OAF=
,cos∠OAF= ;
; 可解得:D(4,-3);
可解得:D(4,-3); ;
; ,
, 、
、
 ,-
,-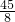 ).
). (3)设圆心O′的坐标为(1,y),则:O′A2=9+y2、O′C2=1+(y-4)2=y2-8y+17,
(3)设圆心O′的坐标为(1,y),则:O′A2=9+y2、O′C2=1+(y-4)2=y2-8y+17, ;
; ∠MNB,
∠MNB,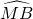 的中点,即:
的中点,即: =
= ;
; =
= ),∠HMG=∠ESA=90°,
),∠HMG=∠ESA=90°, =
= ,即:
,即: =HG=2R…①;
=HG=2R…①; =
= 、
、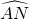 =
= ,
,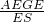 =2R=2
=2R=2 ;
;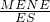 =2
=2 ;
;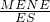 值不会发生变化,且值为2
值不会发生变化,且值为2 .
.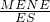 的值,所以可以由与ES相关的相似三角形来解;由∠EAB=
的值,所以可以由与ES相关的相似三角形来解;由∠EAB= ∠MNB可知,直线AE正好经过劣弧MB的中点(设中点为G),过点G作直径GH,连接HM、MG,显然△HMG也是直角三角形,且∠MHG=∠CAB(它们对应的是相等的劣弧),那么Rt△MHG∽Rt△SAE,可得到的是MG:2R=ES:AE,即
∠MNB可知,直线AE正好经过劣弧MB的中点(设中点为G),过点G作直径GH,连接HM、MG,显然△HMG也是直角三角形,且∠MHG=∠CAB(它们对应的是相等的劣弧),那么Rt△MHG∽Rt△SAE,可得到的是MG:2R=ES:AE,即 =2R,而ME•NE=AE•EG,所以只需判断出MG和EG的数量关系就能确定该题的结论,通过观察图形,可以猜测的结论是MG=EG,即需要求证的是∠GME=∠GEM;∠GME对应的是劣弧NG(即
=2R,而ME•NE=AE•EG,所以只需判断出MG和EG的数量关系就能确定该题的结论,通过观察图形,可以猜测的结论是MG=EG,即需要求证的是∠GME=∠GEM;∠GME对应的是劣弧NG(即 和
和 ),而∠GEM=∠MAG+∠AMN(三角形外角的性质),那么∠GEM对应的是
),而∠GEM=∠MAG+∠AMN(三角形外角的性质),那么∠GEM对应的是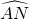 和
和 ;这四段劣弧中,
;这四段劣弧中, =
= ,
,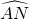 =
= ,所以∠GEM=∠GME,即GM=GE,那么该题的结论已经明确.
,所以∠GEM=∠GME,即GM=GE,那么该题的结论已经明确.

科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com