
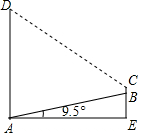
 如图,AB为一斜坡,其坡角为19.5°,紧挨着斜坡AB底部A处有一高楼,一数学活动小组量得斜坡长AB=15m,在坡顶B处测得楼顶D处的仰角为45°,其中测量员小刚的身高BC=1.7米,求楼高AD.
如图,AB为一斜坡,其坡角为19.5°,紧挨着斜坡AB底部A处有一高楼,一数学活动小组量得斜坡长AB=15m,在坡顶B处测得楼顶D处的仰角为45°,其中测量员小刚的身高BC=1.7米,求楼高AD.分析 作CF⊥AD于点F,在直角△ABE中求得BE,和AE的长,然后在直角△CDE中利用三角函数求得DE的长,根据AD=DF+AF=CF+BC+BE求解.
解答 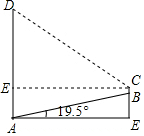 解:作CF⊥AD于点F.
解:作CF⊥AD于点F.
在Rt△ABE中,∵AB=15,
∴BE=ABsin19.5°=15sin19.5°,
AE=ABcos19.5°=15cos19.5°,
在Rt△CDF中,∵CF=AE,∠DCF=45°,
∴DF=CF,
∴AD=DF+AF=CF+BC+BE=15cos19.5°+1.7+15sin19.5°≈21.0(m).
答:楼高AD为21.0米.
点评 本题考查了解直角三角形的应用-仰角俯角问题,还考查的知识点有三角函数、直角三角形的性质以及勾股定理等.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:解答题
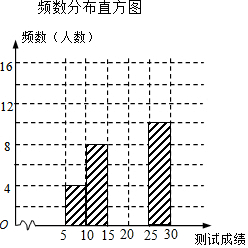 某校为了调查初一年级学生有理数混合运算能力,从七年级400名学生中堆积抽选50名学生参加测试,对这50名学生同时进行30个有理数混合运算的考察,每做正确1个得1分,根据测试成绩绘制出不完整的频数分布直方图如下图表:
某校为了调查初一年级学生有理数混合运算能力,从七年级400名学生中堆积抽选50名学生参加测试,对这50名学生同时进行30个有理数混合运算的考察,每做正确1个得1分,根据测试成绩绘制出不完整的频数分布直方图如下图表:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 5≤x<10 | 4 |
| 第2组 | 10≤x<15 | 8 |
| 第3组 | 15≤x<20 | 16 |
| 第4组 | 20≤x<25 | a |
| 第5组 | 25≤x<30 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | ||
| C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com