
【题目】如图,![]() 的直径
的直径![]() 的长为
的长为![]() ,弦
,弦![]() 长为
长为![]() ,
,![]() 的平分线交
的平分线交![]() 于
于![]() ,则
,则![]() 长为( )
长为( )

A. 7 B. 7![]() C. 8
C. 8![]() D. 9
D. 9
【答案】B
【解析】
作DF⊥CA,交CA的延长线于点F,作DG⊥CB于点G,连接DA,DB.由CD平分∠ACB,根据角平分线的性质得出DF=DG,由HL证明△AFD≌△BGD,△CDF≌△CDG,得出CF=7,又△CDF是等腰直角三角形,从而求出CD=7![]() .
.
作DF⊥CA,垂足F在CA的延长线上,作DG⊥CB于点G,连接DA,DB,
∵CD平分∠ACB,
∴∠ACD=∠BCD
∴DF=DG,![]() ,
,
∴DA=DB,
∵∠AFD=∠BGD=90°,
∴△AFD≌△BGD,
∴AF=BG.
易证△CDF≌△CDG,
∴CF=CG,
∵AC=6,BC=8,
∴AF=1,
∴CF=7,
∵△CDF是等腰直角三角形,
∴CD=7![]() ,
,
故选B.


科目:初中数学 来源: 题型:
【题目】已知:等腰三角形OAB在直角坐标系中的位置如图,点A的坐标为(-3![]() ,3),点B的坐标为(﹣6,0).
,3),点B的坐标为(﹣6,0).
(1)若三角形OAB关于y轴的轴对称图形是三角形OA′B′,请直接写出A、B的对称点A′、B′的坐标;
(2)若将三角形OAB沿x轴向右平移a个单位,此时点A恰好落在反比例函数y=![]() 的图象上,求a的值;
的图象上,求a的值;
(3)若三角形OAB绕点O按逆时针方向旋转α度(0<α<90).
①当α=30°时点B恰好落在反比例函数y=![]() 的图象上,求k的值;
的图象上,求k的值;
②问点A、B能否同时落在①中的反比例函数的图象上,若能,求出α的值;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一出租车一天下午以鼓楼为出发地在东西方向运营,向东走为正,向西走为负,行车里程(单位:㎞)依先后次序记录如下:+9,-3,-5,+4,-8,+6,-3,-6,-4,+10.
⑴将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
⑵若每千米的价格为2.4元,司机一个下午的营业额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D、E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′;
(1)求证:△ABD≌△ACD′;
(2)若∠BAC=120°,求∠DAE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线 y1=﹣2x2+2,直线 y2=2x+2,当 x 任取一值时,x 对应的函数值分别为 y1、y2.若 y1≠y2,取 y1、y2 中的较小值记为 M;若 y1=y2,记 M=y1=y2.例如;当 x=1 时,y1=0,y2=4,y1<y2, 此时 M=0,下列判断中正确的是( )

①当 x>0 时,y1>y2;②当 x<0 时,x 值越大,M 值越小;③使得 M 大于 2 的 x 值不存在;④使得 M=1 的 x 值是﹣![]() 或
或![]() .
.
A. ①②③ B. ①④ C. ②③④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若 x 满足 (9x)(x4)=4, 求 (4x)2+(x9)2 的值.
设 9x=a,x4=b, 则 (9x)(x4)=ab=4,a+b=(9x)+(x4)=5 ,
∴(9x)2+(x4)2=a2+b2=(a+b)22ab=522×4=13
请仿照上面的方法求解下面问题:
(1)若 x 满足 (5x)(x2)=2, 求 (5x)2+(x2)2 的值
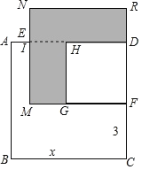
(2)已知正方形 ABCD 的边长为 x , E , F 分别是 AD 、 DC 上的点,且 AE=1 , CF=3 ,长方形 EMFD 的面积是 48 ,分别以 MF 、 DF 作正方形,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示.根据图象解答下列问题:

(1)洗衣机的进水时间是多少分钟?清洗时洗衣机中水量为多少升?
(2)已知洗衣机的排水速度为每分钟19升.
①求排水时洗衣机中的水量y(升)与时间x(分钟)与之间的关系式;
②如果排水时间为2分钟,求排水结束时洗衣机中剩下的水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知![]() 是直角三角形,
是直角三角形,![]() ,
,![]() ,直线l经过点
,直线l经过点![]() ,分别从点
,分别从点![]() 、
、![]() 向直线l作垂线,垂足分别为
向直线l作垂线,垂足分别为![]() 、
、![]() .当点
.当点![]() ,
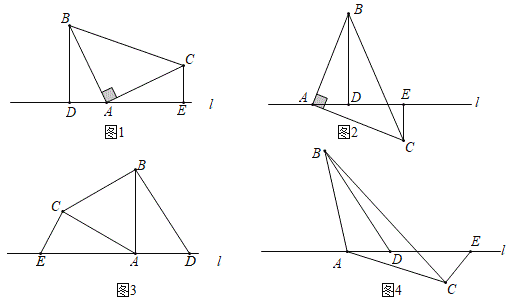
,![]() 位于直线l的同侧时(如图
位于直线l的同侧时(如图![]() ,易证
,易证![]() .如图2,若点
.如图2,若点![]() 在直线l的异侧,其它条件不变,
在直线l的异侧,其它条件不变,![]() 是否依然成立?若成立,请写出证明过程;若不成立,请说明理由.
是否依然成立?若成立,请写出证明过程;若不成立,请说明理由.
(2)变式一:如图3,![]() 中,
中,![]() ,直线l经过点
,直线l经过点![]() ,点
,点![]() 、
、![]() 分别在直线l上,点
分别在直线l上,点![]() 、
、![]() 位于l的同一侧,如果
位于l的同一侧,如果![]() ,求证:
,求证:![]() .
.
(3)变式二:如图4,![]() 中,依然有
中,依然有![]() ,若点
,若点![]() ,
,![]() 位于l的两侧,如果
位于l的两侧,如果![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com