
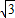 ,∠B为锐角,且关于x的方程x2-4xcosB+1=0有两个相等的实数根.D是劣弧
,∠B为锐角,且关于x的方程x2-4xcosB+1=0有两个相等的实数根.D是劣弧 上任一点(点D不与点A、C重合),DE平分∠ADC,交⊙O于点E,交AC于点F.
上任一点(点D不与点A、C重合),DE平分∠ADC,交⊙O于点E,交AC于点F.
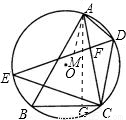
 ;
; BC•AG=6
BC•AG=6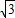 ,
,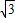 ÷4=3
÷4=3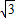 ;
;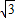 ,则BG=3;
,则BG=3;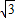 ,由勾股定理,得:
,由勾股定理,得: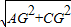 =2
=2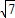 ;
;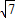 ;
;

 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源:2002年全国中考数学试题汇编《二次函数》(05)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《反比例函数》(01)(解析版) 题型:选择题
查看答案和解析>>
科目:初中数学 来源:2010年中考数学模拟卷(1)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2002年黑龙江省哈尔滨市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2002年黑龙江省哈尔滨市中考数学试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com