
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于D. 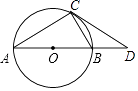
(1)求证:△ADC∽△CDB;
(2)若AC=2,AB= ![]() CD,求⊙O半径.
CD,求⊙O半径.
【答案】
(1)证明:如图,连接CO,
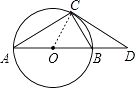 ,
,
∵CD与⊙O相切于点C,
∴∠OCD=90°,
∵AB是圆O的直径,
∴∠ACB=90°,
∴∠ACO=∠BCD,
∵∠ACO=∠CAD,
∴∠CAD=∠BCD,
在△ADC和△CDB中,
![]()
∴△ADC∽△CDB.
(2)解:设CD为x,
则AB= ![]() x,OC=OB=
x,OC=OB= ![]() x,
x,
∵∠OCD=90°,
∴OD= ![]() =
= ![]() =
= ![]() x,
x,
∴BD=OD﹣OB= ![]() x﹣
x﹣ ![]() x=
x= ![]() x,
x,
由(1)知,△ADC∽△CDB,
∴ ![]() =
= ![]() ,
,
即 ![]() ,
,
解得CB=1,
∴AB= ![]() =
= ![]() ,
,
∴⊙O半径是 ![]()
【解析】(1)首先连接CO,根据CD与⊙O相切于点C,可得:∠OCD=90°;然后根据AB是圆O的直径,可得:∠ACB=90°,据此判断出∠CAD=∠BCD,即可推得△ADC∽△CDB.(2)首先设CD为x,则AB= ![]() x,OC=OB=
x,OC=OB= ![]() x,用x表示出OD、BD;然后根据△ADC∽△CDB,可得:
x,用x表示出OD、BD;然后根据△ADC∽△CDB,可得: ![]() =
= ![]() ,据此求出CB的值是多少,即可求出⊙O半径是多少.
,据此求出CB的值是多少,即可求出⊙O半径是多少.
【考点精析】利用切线的性质定理对题目进行判断即可得到答案,需要熟知切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】求1+2+22+23+…+22018的值,可令S=1+2+22+23+…+22018,则2S=2+22+23+24+…22019,因此2S﹣S=22019﹣1,即S=22019﹣1.依照以上的方法,计算出1+5+52+53+…52017的值为( )
A. 52018﹣1 B. 52019﹣1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某糕点厂中秋节前要制作一批盒装月饼,每盒装1个大月饼和7个小月饼,制作1个大月饼要用0.06kg面粉,1个小月饼要用0.015kg面粉,现共有面粉330kg,制作两种月饼各用多少kg面粉时,才能使生产的大小月饼刚好配套成盒?最多能生产多少盒月饼?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O上,点P是直径AB上的一点(不与A重合),过点P作AB的垂线交BC于点Q. 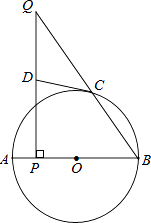
(1)在线段PQ上取一点D,使DQ=DC,连接DC,试判断CD与⊙O的位置关系,并说明理由.
(2)若cosB= ![]() ,BP=6,AP=1,求QC的长.
,BP=6,AP=1,求QC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
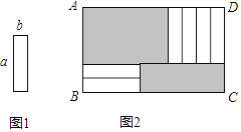
A. a=2b B. a=3b C. a=4b D. a=b
查看答案和解析>>
科目:初中数学 来源: 题型:
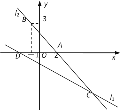
【题目】如图,直线l1的函数关系式为y=-![]() x-1,且l1与x轴交于点D,直线l2经过点A(2,0),B(-1,3),直线l1与l2交于点C.
x-1,且l1与x轴交于点D,直线l2经过点A(2,0),B(-1,3),直线l1与l2交于点C.
(1)求直线l2的函数关系式;
(2)点C的坐标为 ;
(3)求△ADC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com