
 已知,(如图)在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BF上,PM⊥AD于M,
已知,(如图)在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BF上,PM⊥AD于M,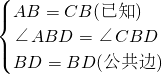 ,
,

 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
| BP |
| PO |
| 1 |
| 3 |
| CP |
| PA |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
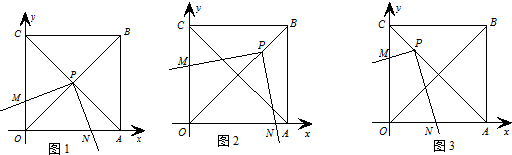
 填空:已知,(如图)在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BF上,PM⊥AD于M,
填空:已知,(如图)在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BF上,PM⊥AD于M,查看答案和解析>>
科目:初中数学 来源:2011年江苏省无锡市前洲中学九年级(下)期中数学试卷(解析版) 题型:解答题
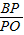 =
= ,直角MPN绕顶点P旋转,角的两边分别与线段OC、OA交于点M、N(不与点C、O、A重合).设CM=a,四边形OMPN的面积为S,则S随a的变化而变化吗?若不变,请求出S的值;若变化,请求出S与a的关系式.
,直角MPN绕顶点P旋转,角的两边分别与线段OC、OA交于点M、N(不与点C、O、A重合).设CM=a,四边形OMPN的面积为S,则S随a的变化而变化吗?若不变,请求出S的值;若变化,请求出S与a的关系式. =
= ,直角MPN绕顶点P旋转,角的两边分别与线段OC、OA交于点M、N(不与点C、O、A重合).设CM=a,四边形OMPN的面积为S=______. (直接写出答案,不需证明;若S随a的变化而不变,直接写出S的值;若变化,直接写出S与a的关系式.)
,直角MPN绕顶点P旋转,角的两边分别与线段OC、OA交于点M、N(不与点C、O、A重合).设CM=a,四边形OMPN的面积为S=______. (直接写出答案,不需证明;若S随a的变化而不变,直接写出S的值;若变化,直接写出S与a的关系式.)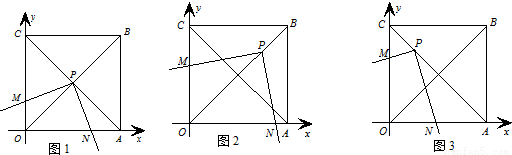
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com