
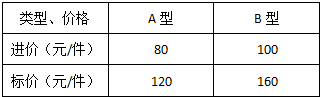
分析 (1)设A种服装购进x件,B种服装购进y件,由总价=单价×数量,利润=售价-进价建立方程组求出其解即可;
(2)设B种服装打m折出售,根据A种服装的利润+B中服装的利润≥2000,求出其解即可.
解答 解:(1)设购进A种服装的件数为x件,B种的为y件,根据题意得:
$\left\{\begin{array}{l}{80x+100y=10000}\\{40x+60y=5400}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=75}\\{y=40}\end{array}\right.$;
(2)设B种服装打m折出售,根据题意得:
(120×0.8-80)×75+(160×$\frac{m}{10}$-100)×40≥2000,
解得:m≥7.5
答:B种服装至多按标价的7.5折出售.
点评 本题考查了一元一次不等式的应用和二元一次方程组解实际问题的运用,解答时由销售问题的数量关系建立二元一次方程组是关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为14cm,则四边形ABFD的周长为( )
如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为14cm,则四边形ABFD的周长为( )| A. | 14cm | B. | 17cm | C. | 20cm | D. | 23cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=180}\\{x=y-60}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=180}\\{x=y+60}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=90}\\{x=y-60}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=90}\\{x=y+60}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3-x>3-y | B. | x-3>y-3 | C. | x+3>y+2 | D. | $\frac{x}{3}$>$\frac{y}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
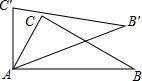 如图所示,在△ABC中,∠CAB=70°,将△ABC绕点A旋转到△A′B′C′的位置,使得C′A⊥AB,则∠BAB′=( )
如图所示,在△ABC中,∠CAB=70°,将△ABC绕点A旋转到△A′B′C′的位置,使得C′A⊥AB,则∠BAB′=( )| A. | 10° | B. | 20° | C. | 30° | D. | 50° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com