
分析 (1)根据题意可以写出每种优惠办法实付金额y1(元),y2(元)与x(本)之间的函数关系式;
(2)根据(1)中函数解析式,可以分别讨论选择“活动1”的优惠办法付款更省钱时x的取值范围;
(3)由题意可知,两种活动都选择最省钱,根据题意目中的条件,可以直接写出最优方案.
解答 解:(1)由题意可得,
当10≤x≤20时,y1=20×15=300,
当x>10时,y1=20×15+5(x-20)=5x+200,
y2=(20×15+5x)×0.8=4x+240,
即y1(元)与x(本)之间的函数关系式是${y}_{1}=\left\{\begin{array}{l}{300}&{(10≤x≤20)}\\{5x+200}&{(x>20)}\end{array}\right.$,
y2(元)与x(本)之间的函数关系式是y2=4x+240;
(2)当10≤x≤20时,令300<4x+240,得15<x≤20,
当x>20时,令5x+200<4x+240,得20<x<40,
由上可得,当15<x<40时,选择“活动1”的优惠办法付款更省钱;
(3)由题意可知,
购买这种钢笔20支和笔记本60本最省钱的购买方案是选择活动1购买20支钢笔,获赠20本笔记本,选择活动2再购买40本笔记本即可.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,写出相应的函数关系式,利用函数的性质和不等式的性质解答.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:解答题
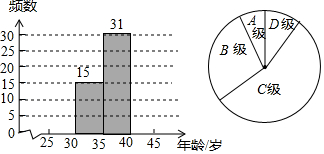 菲尔兹奖是国际上享有崇高声誉的一个数学奖项,每4年评选一次,颁给有卓越贡献的年轻数学家,被视为数学界的诺贝尔奖.下面的数据是从1936年至2014年45岁以下菲尔兹奖得住获奖时的年龄(岁):
菲尔兹奖是国际上享有崇高声誉的一个数学奖项,每4年评选一次,颁给有卓越贡献的年轻数学家,被视为数学界的诺贝尔奖.下面的数据是从1936年至2014年45岁以下菲尔兹奖得住获奖时的年龄(岁):| 分组 | 频数 |
| A:25~30 | 1 |
| B:30~35 | 15 |
| C:35~40 | 31 |
| D:40~45 | 3 |
| 总 计 | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{x}^{2}{y}^{2}}$ | B. | $\sqrt{{x}^{2}+{y}^{2}}$ | C. | $\sqrt{(x+y)^{2}}$ | D. | $\sqrt{x{y}^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
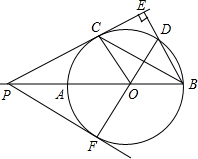 如图,AB是⊙O的直径,延长BA至点P,过点P作⊙O的切线PC,切点为C,过点B向PC的延长线作垂线BE交该延长线于点E,BE交⊙O于点D,已知PA=1,PC=$\sqrt{3}$OC,
如图,AB是⊙O的直径,延长BA至点P,过点P作⊙O的切线PC,切点为C,过点B向PC的延长线作垂线BE交该延长线于点E,BE交⊙O于点D,已知PA=1,PC=$\sqrt{3}$OC,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
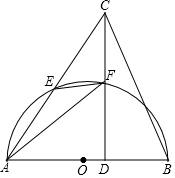 如图,在△ABC中,CD⊥AB,垂足为点D.以AB为直径的半⊙O分别与
如图,在△ABC中,CD⊥AB,垂足为点D.以AB为直径的半⊙O分别与查看答案和解析>>
科目:初中数学 来源: 题型:解答题
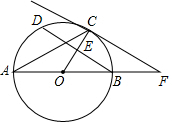 如图,AB为⊙O的直径,CD为⊙O的弦,连接AC、BD,半径CO交BD于点E,过点C作切线,交AB的延长线于点F,且∠CFA=∠DCA.
如图,AB为⊙O的直径,CD为⊙O的弦,连接AC、BD,半径CO交BD于点E,过点C作切线,交AB的延长线于点F,且∠CFA=∠DCA.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com