
【题目】已知抛物线l1:y=﹣x2+2x+3与x轴交于点A、B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,﹣2).
(1)求抛物线l2的解析式;
(2)点P为线段AB上一动点(不与A、B重合),过点P作y轴的平行线交抛物线l1于点M,交抛物线l2于点N.
①当四边形AMBN的面积最大时,求点P的坐标;
②当CM=DN≠0时,求点P的坐标.
【答案】
(1)解:∵令﹣x2+2x+3=0,解得:x1=﹣1,x2=3,
∴A(﹣1,0),B(3,0).
设抛物线l2的解析式为y=a(x+1)(x﹣4).
∵将D(0,﹣2)代入得:﹣4a=﹣2,
∴a= ![]() .
.
∴抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x﹣2
x﹣2
(2)解:①如图1所示:
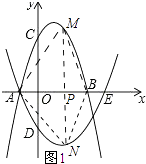
∵A(﹣1,0),B(3,0),
∴AB=4.
设P(x,0),则M(x,﹣x2+2x+3),N(x, ![]() x2﹣
x2﹣ ![]() x﹣2).
x﹣2).
∵MN⊥AB,
∴SAMBN= ![]() ABMN=﹣3x2+7x+10(﹣1<x<3).
ABMN=﹣3x2+7x+10(﹣1<x<3).
∴当x= ![]() 时,SAMBN有最大值.
时,SAMBN有最大值.
∴此时P的坐标为( ![]() ,0).
,0).
②如图2所示:作CG⊥MN于G,DH⊥MN于H,如果CM与DN不平行.
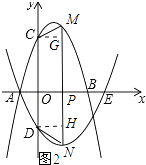
∵DC∥MN,CM=DN,
∴四边形CDNM为等腰梯形.
∴∠DNH=∠CMG.
在△CGM和△DNH中 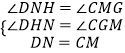 ,
,
∴△CGM≌△DNH.
∴MG=HN.
∴PM﹣PN=1.
设P(x,0),则M(x,﹣x2+2x+3),N(x, ![]() x2﹣
x2﹣ ![]() x﹣2).
x﹣2).
∴(﹣x2+2x+3)+( ![]() x2﹣
x2﹣ ![]() x﹣2)=1,解得:x1=0(舍去),x2=1.
x﹣2)=1,解得:x1=0(舍去),x2=1.
∴P(1,0).
当CM∥DN时,如图3所示:
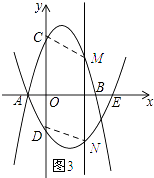
∵DC∥MN,CM∥DN,
∴四边形CDNM为平行四边形.
∴DC=MN=5
∴﹣x2+2x+3﹣( ![]() x2﹣
x2﹣ ![]() x﹣2)=5,
x﹣2)=5,
∴x1=0(舍去),x2= ![]() ,
,
∴P( ![]() ,0).
,0).
总上所述P点坐标为(1,0),或( ![]() ,0)
,0)
【解析】根据二次函数y=﹣x2+2x+3与x轴交于点A、B(点A在点B左边),得到﹣x2+2x+3=0,求出A(﹣1,0),B(3,0),根据抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,﹣2),得到抛物线的解析式;(2)①由AB=4,MN⊥AB,得到SAMBN=![]() ABMN,此时P的坐标为(
ABMN,此时P的坐标为( ![]() ,0);②如图2所示,如果CM与DN不平行,由DC∥MN,CM=DN,得到四边形CDNM为等腰梯形,△CGM≌△DNH,PM﹣PN=1,得到P(1,0);当CM∥DN时,如图3所示,得到四边形CDNM为平行四边形,DC=MN=5,得到P(
,0);②如图2所示,如果CM与DN不平行,由DC∥MN,CM=DN,得到四边形CDNM为等腰梯形,△CGM≌△DNH,PM﹣PN=1,得到P(1,0);当CM∥DN时,如图3所示,得到四边形CDNM为平行四边形,DC=MN=5,得到P(![]() ,0);总上所述P点坐标为(1,0),或(
,0);总上所述P点坐标为(1,0),或(![]() ,0);此题是综合题,难度较大,计算和解方程时需认真仔细.
,0);此题是综合题,难度较大,计算和解方程时需认真仔细.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】小明从A地向南偏东m°(0<m<90)的方向行走到B地,然后向左转30°行走到C地,则下面表述中,正确的个数是( )
①B可能在C的北偏西m°方向;
②当m<60时,B在C的北偏西(m+30)°方向;
③B不可能在C的南偏西m°方向;
④当m>60时,B在C的南偏西(150-m)°方向
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为准备半期考表彰的奖品,计划从友谊超市购买笔记本和水笔共40件.在获知某网店有“双十一”促销活动后,决定从该网店购买这些奖品.已知笔记本和水笔在这两家商店的零售价分别如下表,且在友谊超市购买这些奖品需花费90元.求从网店购买这些奖品可节省多少元.
品 名 商 店 | 笔记本 (元/件) | 水笔 (元/件) |
友谊超市 | 2.4 | 2 |
网 店 | 2 | 1.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500m,先到终点
的人原地休息.已知甲先出发2s.在跑步过程中,甲、乙两人的距离y(m)与乙出发的时间t(s)之间的关系
如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是【 】

A.①②③ B.仅有①② C.仅有①③ D.仅有②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去两次租用这种货车的情况如下表:

现租用该公司3辆甲种货车及5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,货主应付运费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
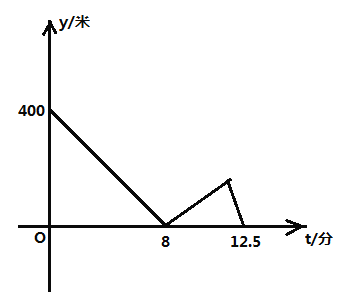
【题目】重庆实验外国语学校每年四月初都定期举办体育文化节,初![]() 届周华同学为了在本次活动中获得更好的成绩,他让父亲带自己进行了体能训练,他们找了条笔直的跑道
届周华同学为了在本次活动中获得更好的成绩,他让父亲带自己进行了体能训练,他们找了条笔直的跑道![]() ,两人都从起点
,两人都从起点![]() 出发且一直保持匀速运动,父亲先出发两分钟后周华才出发,两人到达终点
出发且一直保持匀速运动,父亲先出发两分钟后周华才出发,两人到达终点![]() 后均停止运动,周华与父亲之间的距离
后均停止运动,周华与父亲之间的距离![]() (米)与周华出发的时间
(米)与周华出发的时间![]() (分)的关系如图所示,当周华到达终点时,父亲离终点的距离为________米.
(分)的关系如图所示,当周华到达终点时,父亲离终点的距离为________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=﹣x+b也随之移动,设移动时间为t秒.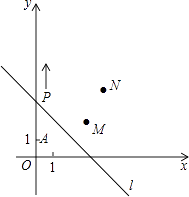
(1)当t=2时,则AP= , 此时点P的坐标是 .
(2)当t=3时,求过点P的直线l:y=﹣x+b的解析式?
(3)当直线l:y=﹣x+b从经过点M到点N时,求此时点P向上移动多少秒?
(4)点Q在x轴时,若S△ONQ=8时,请直按写出点Q的坐标是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com