
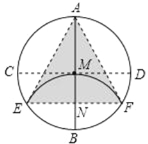
【题目】如图,AB、CD 为圆形纸片中两条互相垂直的直径,将圆形纸片沿EF 折叠,使 B 与圆心 M 重合,折痕 EF 与 AB 相交于 N,连结 AE、AF,得到了以下结论:①四边形 MEBF 是菱形,②△AEF 为等边三角形,③S△AEF:S 圆=3![]() :4π,其中正确的是_______.
:4π,其中正确的是_______.
【答案】①②③
【解析】
①根据垂径定理可得 BM 垂直平分 EF,再求出 BN=MN,从而得到 BM、EF 互相垂直平分,然后根据对角线互相垂直平分的四边形是菱形求出四边形MEBF 是菱形,从而得到①正确;②连接 ME,根据直角三角形 30°角所对的直角边等于斜边的一半求出∠MEN=30°,然后求出∠EMN=60°,根据等边对等角求出∠AEM=∠EAM,然后利用三角形的一个外角等于与它不相邻的两个内角的和求出∠AEM =30°,从而得到∠AEF=60°,同理求出∠AFE=60°,再根据三角形的内角和等于 180°求出∠EAF=60°,从而判定△AEF 是等边三角形,②正确;③设圆的半径为 r,求出 MN=![]() r,EN=
r,EN= ![]() r, 然后求出 AN、EF,再根据三角形的面积公式与圆的公式列式整理即可得到③正确.
r, 然后求出 AN、EF,再根据三角形的面积公式与圆的公式列式整理即可得到③正确.
①根据垂径定理,BM 垂直平分 EF,
又∵纸片沿 EF 折叠,B、M 两点重合,
∴BN=MN,
∴BM、EF 互相垂直平分,
∴四边形 MEBF 是菱形,故①正确;
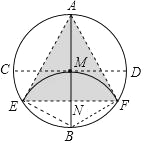
②如图,连接 ME,则 ME=MB=2MN.
∵∠ENM=90°,
∴∠MEN=30°,
∴∠EMN=90°﹣30°=60°,
又∵AM=ME(都是半径),
∴∠AEM=∠EAM,
∴∠AEM=![]() ∠EMN=
∠EMN= ![]() ×60°=30°,
×60°=30°,
∴∠AEF=∠AEM+∠MEN=30°+30°=60°,
同理可求∠AFE=60°,
∴∠EAF=60°,
∴△AEF 是等边三角形,故②正确;
③设圆的半径为 r,则 MN=![]() r,EN=
r,EN= ![]() r,
r,
∴EF=2EN=![]() r,AN=r+
r,AN=r+ ![]() r=
r=![]() r,
r,
∴S△AEF:S 圆=(![]() ×
×![]() r×
r×![]() r):πr2=3
r):πr2=3![]() :4,故③正确;
:4,故③正确;
综上所述,结论正确的是①②③.
故答案①②③.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】一个矩形ABCD的较短边长为2.
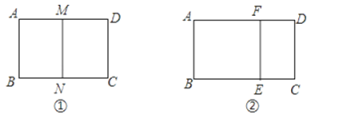
(1)如图①,若沿长边对折后得到的矩形与原矩形相似,求它的另一边长;
(2)如图②,已知矩形ABCD的另一边长为4,剪去一个矩形ABEF后,余下的矩形EFDC与原矩形相似,求余下矩形EFDC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
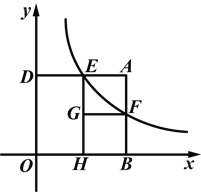
【题目】(2014浙江金华)如图,矩形ABOD的两边OB,OD都在坐标轴的正半轴上,OD=3,另两边与反比例函数![]() (k≠0)的图象分别相交于点E、F,且DE=2.过点E作EH⊥x轴于点H,过点F作FG⊥EH于点G.回答下面的问题:
(k≠0)的图象分别相交于点E、F,且DE=2.过点E作EH⊥x轴于点H,过点F作FG⊥EH于点G.回答下面的问题:
(1)①求反比例函数的解析式.
②当四边形AEGF为正方形时,求点F的坐标.
(2)小亮进一步研究四边形AEGF的特征后提出问题:“当AE>EG时,矩形AEGF与矩形DOHE能否全等?能否相似?”
针对小亮提出的问题,请你判断这两个矩形能否全等(直接写出结论即可).这两个矩形能否相似?若能相似,求出相似比;若不能相似,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
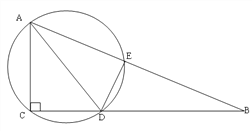
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,CB=8,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE。
(1)求证:AC=AE;
(2)求△ACD外接圆的直径。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个口袋中装有4个完成相同的小球,把它们分别标号1、2、3、4,小明从中随机地摸出一个球.
(1)直接写出小明摸出的球标号为4的概率;
(2)若小明摸到的球不放回,记小明摸出球的标号为x,然后由小强再随机摸出一个球记为y.小明和小强在此基础上共同协商一个游戏规则:当x>y时,小明获胜,否则小强获胜.请问他们制定的游戏规则公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
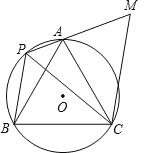
【题目】如图,等边△ABC 内接于⊙O,P 是![]() 上任一点(点 P 不与点 A、B 重合),连 AP、BP,过点 C 作 CM∥BP 交 PA 的延长线于点 M.
上任一点(点 P 不与点 A、B 重合),连 AP、BP,过点 C 作 CM∥BP 交 PA 的延长线于点 M.
(1)填空:∠APC= 度,∠BPC= 度;
(2)求证:△ACM≌△BCP;
(3)若 PA=1,PB=2,求梯形 PBCM 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
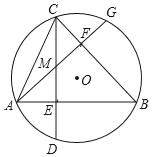
【题目】如图,在圆O中,弦AB⊥CD于E,弦AG⊥BC于F,CD与AG相交于点M.
(1)求证:弧BD=弧BG.
(2)如果AB=12,CM=4,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
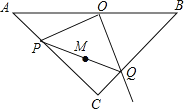
【题目】如图,等腰Rt△ABC中,斜边AB的长为2,O为AB的中点,P为AC边上的动点,OQ⊥OP交BC于点Q,M为PQ的中点,当点P从点A运动到点C时,点M所经过的路线长为( )
A. ![]() B.
B. ![]() C. 1 D. 2
C. 1 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
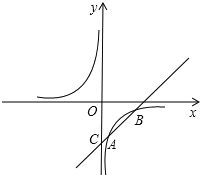
【题目】如图,已知反比例函数y =![]() 的图象经过点A(1,-3),一次函数y =kx +b的图象经过点A与点C(0,-4),且与反比例函数的图象相交于另一点B.试确定点B的坐标.
的图象经过点A(1,-3),一次函数y =kx +b的图象经过点A与点C(0,-4),且与反比例函数的图象相交于另一点B.试确定点B的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com