
【题目】如图,在圆O中,弦AB⊥CD于E,弦AG⊥BC于F,CD与AG相交于点M.
(1)求证:弧BD=弧BG.
(2)如果AB=12,CM=4,求圆O的半径.
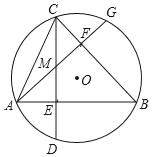
【答案】(1)证明见解析;(2)2![]()
【解析】
(1)连结AD、BD、BG,由AB⊥CD,AG⊥BC得到∠CEB=∠AFB=90°,根据等角的余角相等得到∠ECB=∠BAF,即可得出结论;
(2)连接OA、OB、OC、OG、CG,作OH⊥CG于H,OK⊥AB于K,由垂径定理得出CH=GH=![]() CG,AK=BK=
CG,AK=BK=![]() AB=6,由圆周角定理和角的互余关系证出∠CNF=∠AGC,得出CG=CM=4,因此GH=2,由AG⊥BC证出弧BG的度数+弧AC的度数=180°,得出∠COG+∠AOB=180°,因此∠HOG+∠BOK=90°,证出∠HGO=∠BOK,由AAS证明△HOG≌△KBO,得出对应边相等OK=HG=2,再由勾股定理求出OB即可.
AB=6,由圆周角定理和角的互余关系证出∠CNF=∠AGC,得出CG=CM=4,因此GH=2,由AG⊥BC证出弧BG的度数+弧AC的度数=180°,得出∠COG+∠AOB=180°,因此∠HOG+∠BOK=90°,证出∠HGO=∠BOK,由AAS证明△HOG≌△KBO,得出对应边相等OK=HG=2,再由勾股定理求出OB即可.
(1)证明:连结AD、BD、BG,如图1所示,
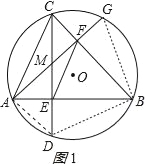
∵AB⊥CD,AG⊥BC,
∴∠CEB=∠AFB=90°,
∴∠ECB+∠B=90°,∠BAF+∠B=90°,
∴∠ECB=∠BAF,即∠DCB=∠BAG,
∴弧BD=弧BG;
(2)解:连接OA、OB、OC、OG、CG,作OH⊥CG于H,OK⊥AB于K,如图2所示:
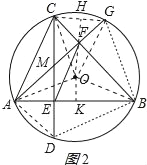
则CH=GH=![]() CG,AK=BK=
CG,AK=BK=![]() AB=6,
AB=6,
∵∠DCB=∠BAG,∠DCB+∠CMF=90°,∠BAG+∠ABF=90°,
∴∠CMF=∠ABF,
∵∠ABF=∠AGC,
∴∠CMF=∠AGC,
∴CG=CM=4,
∴GH=2,
∵AG⊥BC,
∴∠AFB=90°,
∴∠FAB+∠FBA=90°,
∴弧BG的度数+弧AC的度数=180°,
∴∠COG+∠AOB=180°,
∴∠HOG+∠BOK=90°,
∵∠HGO+∠HOG=90°,
∴∠HGO=∠BOK,
在△HOG和△KBO中,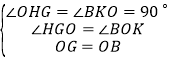 ,
,
∴△HOG≌△KBO(AAS),
∴OK=HG=2,
∴OB=![]() =
=![]() =2
=2![]() ;
;
即⊙O的半径为2![]() .
.


科目:初中数学 来源: 题型:
【题目】按要求完成下列各小题.
(1)解方程:x2+6x+2=2x+7;
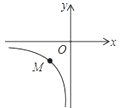
(2)如图是反比例函数y=![]() 在第三象限的图案,点M在该图象上,且点M到点x轴,y轴的距离都等于|k|,求k的值.
在第三象限的图案,点M在该图象上,且点M到点x轴,y轴的距离都等于|k|,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
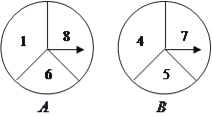
【题目】如图,有两个可以自由转动的均匀转盘A,B,都被分成3等份,每份内均标有数字,小明和小亮用这两个转盘做游戏,游戏规则如下:分别转动转盘A和B,两个转盘停止后,将两个指针所指份内的数字相加(如果指针恰好停在等分线上,那么重转一次,直到指针指向某一份为止),若和为偶数,则小明获胜;如果和为奇数,那么小亮获胜.
(1)请画出树状图,求小明获胜的概率P(A)和小亮获胜的概率P(B).
(2)通过(1)的计算结果说明该游戏的公平性.
查看答案和解析>>
科目:初中数学 来源: 题型:
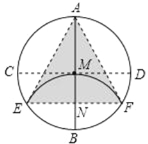
【题目】如图,AB、CD 为圆形纸片中两条互相垂直的直径,将圆形纸片沿EF 折叠,使 B 与圆心 M 重合,折痕 EF 与 AB 相交于 N,连结 AE、AF,得到了以下结论:①四边形 MEBF 是菱形,②△AEF 为等边三角形,③S△AEF:S 圆=3![]() :4π,其中正确的是_______.
:4π,其中正确的是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
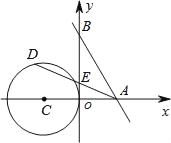
【题目】如图,已知直线y=-![]() x+2
x+2![]() 与两坐标轴分别交于A、B两点,⊙C的圆心坐标为(﹣2,0),半径为2,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积S的取值范围是_____.
与两坐标轴分别交于A、B两点,⊙C的圆心坐标为(﹣2,0),半径为2,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积S的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
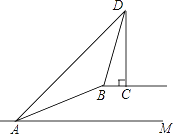
【题目】如图,斜坡AB的坡度为1:2.4,长度为26m,在坡顶B所在的平台上有一座电视塔CD,已知在A处测得塔顶D的仰角为45°,在B处测得塔顶D的仰角为73°,求电视塔CD的高度. (参考数值:sin73°≈ ![]() ,cos73°≈0.
,cos73°≈0. ![]() ,tan73°≈
,tan73°≈ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列问题,列出关于![]() 的方程,并将其化为一元二次方程的一般形式
的方程,并将其化为一元二次方程的一般形式
(1)有一个三位数,它的个位数字比十位数字大![]() ,十位数字比百位数字小
,十位数字比百位数字小![]() ,三个数字的平方和的
,三个数字的平方和的![]() 倍比这个三位数小
倍比这个三位数小![]() ,求这个三位数.
,求这个三位数.
(2)如果一个直角三角形的两条直角边长之和为![]() ,面积为
,面积为![]() ,求它的两条直角边的长.
,求它的两条直角边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
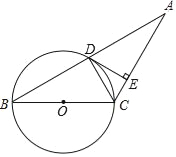
【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过点D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接DC,若BC=4,求弧DC与弦DC所围成的图形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com