
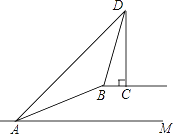
【题目】如图,斜坡AB的坡度为1:2.4,长度为26m,在坡顶B所在的平台上有一座电视塔CD,已知在A处测得塔顶D的仰角为45°,在B处测得塔顶D的仰角为73°,求电视塔CD的高度. (参考数值:sin73°≈ ![]() ,cos73°≈0.
,cos73°≈0. ![]() ,tan73°≈
,tan73°≈ ![]() )
)
【答案】电视塔CD的高度为20m
【解析】
延长DC 交AM于F,作BE⊥AM于E.首先证明四边形BCEF是矩形,由题意BE:AE=1:2.4,在Rt△ABE中,根据AB=26,由勾股定理可得BE=10,AE=24,在Rt△BCD中,可知tan73°=![]() ,推出
,推出![]() ,推出DC=
,推出DC=![]() BC,在Rt△AFD中,由∠DAF=45°,可知AF=DF,可得24+BC=10+
BC,在Rt△AFD中,由∠DAF=45°,可知AF=DF,可得24+BC=10+![]() BC,解方程求出BC即可解决问题.
BC,解方程求出BC即可解决问题.
解:延长DC 交AM于F,作BE⊥AM于E.
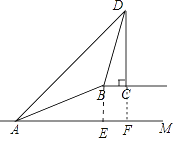
∵DF⊥BC,DF⊥AM,
∴∠AEB=∠AFD=∠DCB=∠BCF=90°,
∴四边形BCEF是矩形,
∴BC=EF,BE=CF,
由题意BE:AE=1:2.4,
在Rt△ABE中,∵AB=26,
由勾股定理可得BE=10,AE=24,
在Rt△BCD中,∵∠DBC=73°,
∴tan73°=![]() ,
,
∴ ![]() ,
,
∴DC= ![]() BC,
BC,
在Rt△AFD中,∵∠DAF=45°,
∴AF=DF,
∴24+BC=10+ ![]() BC,
BC,
∴BC=6,DC=20,
答:电视塔CD的高度为20m


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
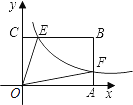
【题目】如图,已知双曲线 ![]() (x>0)经过矩形OABC的边AB、BC上的点F、E,其中CE=
(x>0)经过矩形OABC的边AB、BC上的点F、E,其中CE= ![]() CB,AF=
CB,AF= ![]() AB,且四边形OEBF的面积为2,则k的值为________.
AB,且四边形OEBF的面积为2,则k的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
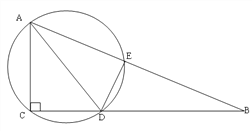
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,CB=8,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE。
(1)求证:AC=AE;
(2)求△ACD外接圆的直径。
查看答案和解析>>
科目:初中数学 来源: 题型:
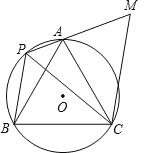
【题目】如图,等边△ABC 内接于⊙O,P 是![]() 上任一点(点 P 不与点 A、B 重合),连 AP、BP,过点 C 作 CM∥BP 交 PA 的延长线于点 M.
上任一点(点 P 不与点 A、B 重合),连 AP、BP,过点 C 作 CM∥BP 交 PA 的延长线于点 M.
(1)填空:∠APC= 度,∠BPC= 度;
(2)求证:△ACM≌△BCP;
(3)若 PA=1,PB=2,求梯形 PBCM 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
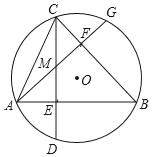
【题目】如图,在圆O中,弦AB⊥CD于E,弦AG⊥BC于F,CD与AG相交于点M.
(1)求证:弧BD=弧BG.
(2)如果AB=12,CM=4,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
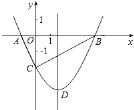
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A,B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A,B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当MC+MA的值最小时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
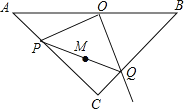
【题目】如图,等腰Rt△ABC中,斜边AB的长为2,O为AB的中点,P为AC边上的动点,OQ⊥OP交BC于点Q,M为PQ的中点,当点P从点A运动到点C时,点M所经过的路线长为( )
A. ![]() B.
B. ![]() C. 1 D. 2
C. 1 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标(4,0),其部分图象如图所示,下列结论:①抛物线过原点;②a﹣b+c<0;③4a+b+c=0;④抛物线的顶点坐标为(2,b);⑤当x<1时,y随x增大而增大.其中结论正确的是( )
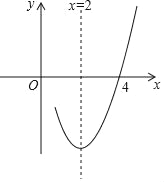
A. ①②③ B. ①④⑤ C. ①③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC,∠B=90°,点P由A开始沿AB向B运动,速度是1cm/s,点Q由B开始沿BC向C运动,速度是2cm/s,如果P、Q同时出发,经过多长时间△PBQ的面积等于7cm2,请列出方程估计解的大致范围(误差不超过0.01s).
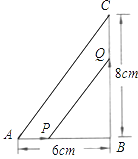
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com