
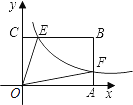
【题目】如图,已知双曲线 ![]() (x>0)经过矩形OABC的边AB、BC上的点F、E,其中CE=
(x>0)经过矩形OABC的边AB、BC上的点F、E,其中CE= ![]() CB,AF=
CB,AF= ![]() AB,且四边形OEBF的面积为2,则k的值为________.
AB,且四边形OEBF的面积为2,则k的值为________.
科目:初中数学 来源: 题型:
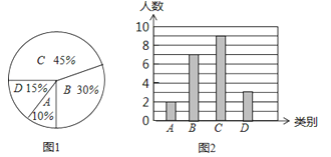
【题目】某校要求340名学生进行社会调查,每人须完成3﹣6份报告.调查结束后随机抽查了20名学生每人完成报告的份数,并分为四类,A:3份;B:4份;C:5份;D:6份.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误.
回答问题:
(1)写出条形图中存在的错误,并说明理由;
(2)写出这20名学生每人完成报告份数的众数、中位数;
(3)在求这20名学生每人完成报告份数的平均数时,小静是这样分析的:
第一步求平均数的公式是![]() =
=![]() ;
;
第二步在该问题中,n=4,x1=3,x2=4,x3=5,x4=6;
第三步:![]() =
=![]() =4.5(份)
=4.5(份)
①小静的分析是从哪一步开始出现错误的?
②请你帮她计算出正确的平均数,并估计这340名学生共完成报告多少份.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有红、黄两个盒子,红盒子中装有编号分别为1、2、3、4的四个红球,黄盒子中装有编号为1、2、3的三个黄球.甲、乙两人玩摸球游戏,游戏规则为:甲从红盒子中每次摸出一个小球,乙从黄盒子中每次摸出一个小球,若两球编号之和为奇数,则甲胜,否则乙胜.
(1)试用列表或画树形图的方法,求甲获胜的概率;
(2)请问这个游戏规则对甲、乙双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
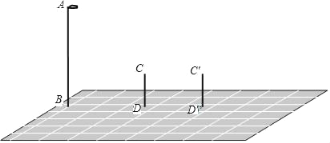
【题目】如图,AB表示路灯,CD、C′D′表示小明所在两个不同位置:
(1)分别画出这两个不同位置小明的影子;
(2)小明发现在这两个不同的位置上,他的影子长分别是自己身高的1倍和2倍,他又量得自己的身高为1.5米,DD′长为3米,你能帮他算出路灯的高度吗?(B、D、D′在一条直线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求完成下列各小题.
(1)解方程:x2+6x+2=2x+7;
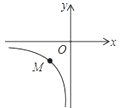
(2)如图是反比例函数y=![]() 在第三象限的图案,点M在该图象上,且点M到点x轴,y轴的距离都等于|k|,求k的值.
在第三象限的图案,点M在该图象上,且点M到点x轴,y轴的距离都等于|k|,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
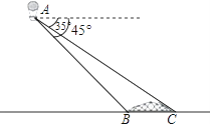
【题目】小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,求热气球离地面的高度.(结果保留整数)(参考数据:sin35°=0.57,cos35°=0.82,tan35°=0.70)
查看答案和解析>>
科目:初中数学 来源: 题型:
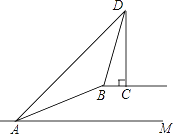
【题目】如图,斜坡AB的坡度为1:2.4,长度为26m,在坡顶B所在的平台上有一座电视塔CD,已知在A处测得塔顶D的仰角为45°,在B处测得塔顶D的仰角为73°,求电视塔CD的高度. (参考数值:sin73°≈ ![]() ,cos73°≈0.
,cos73°≈0. ![]() ,tan73°≈
,tan73°≈ ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com