
【题目】如图是由边长为1的小正方形组成的网格.
(1)求四边形ABCD的面积;
(2)你能判断AD与CD的位置关系吗?说出你的理由.

【答案】(1)12.5;(2)AD与CD互相垂直,理由见解析.
【解析】
(1)根据四边形ABCD的面积=大正方形的面积-四个小直角三角形的面积计算即可;(2)AD⊥DC,利用勾股定理的逆定理证明△ADC是直角三角形即可.
解:(1)四边形ABCD的面积可看作是边长为5的正方形的面积与四个角上的四个直角三角形的面积之差,于是四边形ABCD的面积等于52-(![]() ×3×3+
×3×3+![]() ×2×3+
×2×3+![]() ×4×2+
×4×2+![]() ×1×2)=12.5.
×1×2)=12.5.
(2)AD与CD互相垂直.理由如下:
连接AC,由勾股定理,可得AD2=12+22=5,CD2=22+42=20,又∵AC2=52=25,
∴AD2+CD2=AC2,
∴∠ADC=90°,
即AD与CD互相垂直.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”,2017年1月,某公司向深圳市场新投放共享单车640辆.
(1)若1月份到4月份新投放单车数量的月平均增长率相同,3月份新投放共享单车1000辆.请问该公司4月份在深圳市新投放共享单车多少辆?
(2)考虑到自行车市场需求不断增加,某商城准备用不超过70000元的资金再购进A,B两种规格的自行车100辆,已知A型的进价为500元/辆,售价为700元/辆,B型车进价为1000元/辆,售价为1300元/辆。假设所进车辆全部售完,为了使利润最大,该商城应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
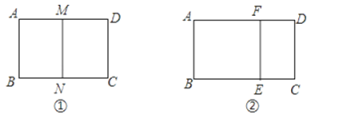
【题目】一个矩形ABCD的较短边长为2.
(1)如图①,若沿长边对折后得到的矩形与原矩形相似,求它的另一边长;
(2)如图②,已知矩形ABCD的另一边长为4,剪去一个矩形ABEF后,余下的矩形EFDC与原矩形相似,求余下矩形EFDC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
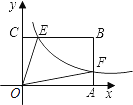
【题目】如图,已知双曲线 ![]() (x>0)经过矩形OABC的边AB、BC上的点F、E,其中CE=
(x>0)经过矩形OABC的边AB、BC上的点F、E,其中CE= ![]() CB,AF=
CB,AF= ![]() AB,且四边形OEBF的面积为2,则k的值为________.
AB,且四边形OEBF的面积为2,则k的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.

(1)判断AB、AE的数量关系,并说明理由;
(2)求两个岛屿A和B之间的距离(结果精确到0.1km).
(参考数据:≈1.73,sin74°≈,cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请判断下列问题中,哪些是反比例函数,并说明你的依据.
(1)三角形的底边一定时,它的面积和这个底边上的高;
(2)梯形的面积一定时,它的中位线与高;
(3)当矩形的周长一定时,该矩形的长与宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2014浙江金华)如图,矩形ABOD的两边OB,OD都在坐标轴的正半轴上,OD=3,另两边与反比例函数![]() (k≠0)的图象分别相交于点E、F,且DE=2.过点E作EH⊥x轴于点H,过点F作FG⊥EH于点G.回答下面的问题:
(k≠0)的图象分别相交于点E、F,且DE=2.过点E作EH⊥x轴于点H,过点F作FG⊥EH于点G.回答下面的问题:
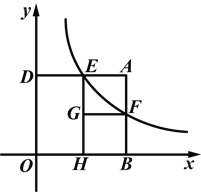
(1)①求反比例函数的解析式.
②当四边形AEGF为正方形时,求点F的坐标.
(2)小亮进一步研究四边形AEGF的特征后提出问题:“当AE>EG时,矩形AEGF与矩形DOHE能否全等?能否相似?”
针对小亮提出的问题,请你判断这两个矩形能否全等(直接写出结论即可).这两个矩形能否相似?若能相似,求出相似比;若不能相似,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
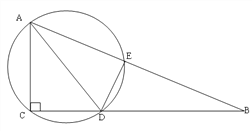
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,CB=8,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE。
(1)求证:AC=AE;
(2)求△ACD外接圆的直径。
查看答案和解析>>
科目:初中数学 来源: 题型:
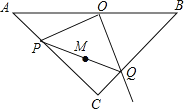
【题目】如图,等腰Rt△ABC中,斜边AB的长为2,O为AB的中点,P为AC边上的动点,OQ⊥OP交BC于点Q,M为PQ的中点,当点P从点A运动到点C时,点M所经过的路线长为( )
A. ![]() B.
B. ![]() C. 1 D. 2
C. 1 D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com