
【题目】请判断下列问题中,哪些是反比例函数,并说明你的依据.
(1)三角形的底边一定时,它的面积和这个底边上的高;
(2)梯形的面积一定时,它的中位线与高;
(3)当矩形的周长一定时,该矩形的长与宽.
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
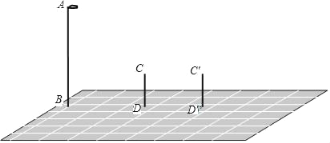
【题目】如图,AB表示路灯,CD、C′D′表示小明所在两个不同位置:
(1)分别画出这两个不同位置小明的影子;
(2)小明发现在这两个不同的位置上,他的影子长分别是自己身高的1倍和2倍,他又量得自己的身高为1.5米,DD′长为3米,你能帮他算出路灯的高度吗?(B、D、D′在一条直线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,求热气球离地面的高度.(结果保留整数)(参考数据:sin35°=0.57,cos35°=0.82,tan35°=0.70)
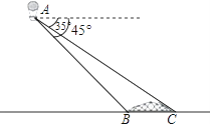
查看答案和解析>>
科目:初中数学 来源: 题型:
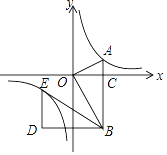
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(![]() ,1)在反比例函数y=
,1)在反比例函数y=![]() 的图象上.
的图象上.
(1)求k的值;
(2)若将△BOA绕点B按逆时针方向旋转60°,得到△BDE,判断点E是否在该反比例函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数,试问:按这种方法能组成哪些位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习苏科版九下《锐角三角函数》一章时,小明同学对一个角的倍角的三角函数值是否具有关系产生了浓厚的兴趣,进行了一些研究.
(1)初步尝试:我们知道:tan60°= ,tan30°= ,发现结论:tanA 2tan![]() ∠A(填“=”或“≠”);
∠A(填“=”或“≠”);
(2)实践探究:如图1,在Rt△ABC中,∠C=90°,AC=2,BC=1,求tan![]() ∠A的值;小明想构造包含
∠A的值;小明想构造包含![]() ∠A的直角三角形:延长CA至D,使得DA=AB,连接BD,所以得到∠D=
∠A的直角三角形:延长CA至D,使得DA=AB,连接BD,所以得到∠D=![]() ∠A,即转化为求∠D的正切值.
∠A,即转化为求∠D的正切值.
请按小明的思路进行余下的求解:
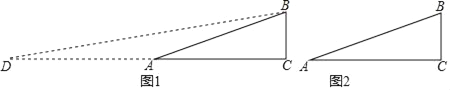
(3)拓展延伸:如图2,在Rt△ABC中,∠C=90°,AC=3,tanA=![]() .
.
①tan2A= ;
②求tan3A的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com