
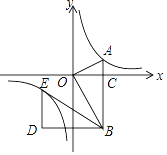
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(![]() ,1)在反比例函数y=
,1)在反比例函数y=![]() 的图象上.
的图象上.
(1)求k的值;
(2)若将△BOA绕点B按逆时针方向旋转60°,得到△BDE,判断点E是否在该反比例函数的图象上,并说明理由.
【答案】(1)k=![]() ;点E在该反比例函数的图像上,理由见解析.
;点E在该反比例函数的图像上,理由见解析.
【解析】
(1)把A(![]() ,1)代入反比例函数y=
,1)代入反比例函数y=![]() ,求k;(2)由勾股定理求出AO,再证△AOC∽△ABO,得
,求k;(2)由勾股定理求出AO,再证△AOC∽△ABO,得![]() ,求出AB,OB,由sin∠ABO=
,求出AB,OB,由sin∠ABO=![]() =
=![]() ,求出∠ABO=30°,由旋转性质求得OB=BD=2
,求出∠ABO=30°,由旋转性质求得OB=BD=2![]() ,OA=DE=2,再求得BD-OC=2
,OA=DE=2,再求得BD-OC=2![]() -
-![]() ,BC-DE=1,故E(-
,BC-DE=1,故E(-![]() ,-1).可判断E的位置.
,-1).可判断E的位置.
解:(1)∵点A(![]() ,1)在反比例函数y=
,1)在反比例函数y=![]()
的图像上,∴k=![]() ×1=
×1=![]() .
.
(2)点E在该反比例函数的图像上.理由如下:
∵A(![]() ,1)
,1)
∴AO=![]() =2.
=2.
由AO⊥OB,AB⊥x轴,易证△AOC∽△ABO,
∴![]() ,即
,即![]() ,
,
∴AB=4,
∴OB=![]()
=![]() =2
=2![]() ,
,
∴sin∠ABO=![]() =
=![]() ,
,
∴∠ABO=30°.由旋转可知△BOA≌△BDE,∠OBD=60°,
∴OB=BD=2![]() ,OA=DE=2,∠BOA=∠BDE=90°,∠ABD=30°+60°=90°.
,OA=DE=2,∠BOA=∠BDE=90°,∠ABD=30°+60°=90°.
又BD-OC=2![]() -
-![]() =
=![]() ,BC-DE=4-1-2=1,∴E(-
,BC-DE=4-1-2=1,∴E(-![]() ,-1).
,-1).
∵-![]() ×(-1)=
×(-1)=![]() ,
,
∴点E在该反比例函数的图像上.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
【题目】小明在操场上做游戏,他发现地上有一个不规则的封闭图形ABC.为了知道它的面积,他在封闭图形内划出了一个半径为1米的圆,在不远处向图形内掷石子,且记录如下:

(1)随着次数的增多,小明发现m与n的比值在一个常数k附近波动,请你写出k的值。
(2)请利用学过的知识求出封闭图形ABC的大致面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ADF和△BCE中,∠A=∠B,点D、E、F、C在同﹣直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF。
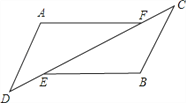
(1)请用其中两个关系式作为条件,另一个作为结论,写出所有你认为正确的命题.(用序号写出命题书写形式,如:如果①、②,那么③)
(2)选择(1)中你写出的一个命题,说明它正确的理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ACDF中,AC=DF,点B在CD上,点E在DF上,BC=DE=a,AC=BD=b,AB=BE=c,且AB⊥BE.
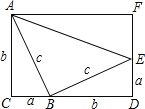
(1)用两种不同的方法表示出长方形ACDF的面积S,并探求a,b,c之间的等量关系(需要化简)
(2)请运用(1)中得到的结论,解决下列问题:
①求当c=5,a=3时,求S的值;
②当c﹣b=8,a=12时,求S的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,AB=12厘米,BC=8厘米,CD=14厘米,∠B=∠C,点E为线段AB的中点.如果点P在线段BC上以3厘米秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为_____厘米/秒时,能够使△BPE与以C、P、Q三点所构成的三角形全等.
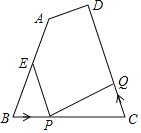
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(2,2),反比例函数![]() (x>0,k≠0)的图像经过线段BC的中点D.
(x>0,k≠0)的图像经过线段BC的中点D.

(1)求k的值;
(2)若点P(x,y)在该反比例函数的图像上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的解析式并写出x的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条不完整的数轴上从左到右有点![]() ,其中点
,其中点![]() 到点
到点![]() 的距离为3,点
的距离为3,点![]() 到点
到点![]() 的距离为7,如图所示:设点
的距离为7,如图所示:设点![]() 所对应的数的和是
所对应的数的和是![]() .
.
(1)若以![]() 为原点,则
为原点,则![]() 的值是 .
的值是 .
(2)若原点![]() 在图中数轴上,且点
在图中数轴上,且点![]() 到原点
到原点![]() 的距离为4,求
的距离为4,求![]() 的值.
的值.
(3)动点![]() 从
从![]() 点出发,以每秒2个单位长度的速度向终点
点出发,以每秒2个单位长度的速度向终点![]() 移动,动点
移动,动点![]() 同时从
同时从![]() 点出发,以每秒1个单位的速度向终点
点出发,以每秒1个单位的速度向终点![]() 移动,当几秒后,
移动,当几秒后,![]() 两点间的距离为2?(直接写出答案即可)
两点间的距离为2?(直接写出答案即可)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
|
|
|
|
|
| ··· |
![]() 可求得
可求得![]() ,第
,第![]() 个格子中的数为 ;
个格子中的数为 ;
![]() 判断:前
判断:前![]() 个格子中所填整数之和是否可能为
个格子中所填整数之和是否可能为![]() 若能,求出
若能,求出![]() 的值,若不可能,请说明理由;
的值,若不可能,请说明理由;
![]() 如果
如果![]() ,
,![]() 为前
为前![]() 格子中的任意两个数,那么所有
格子中的任意两个数,那么所有![]() 的和可以通过计算
的和可以通过计算
![]() 得到,若
得到,若![]() span>,
span>,![]() 为前
为前![]() 格子中的任意两个数,则所有
格子中的任意两个数,则所有![]() 的的和为
的的和为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com