
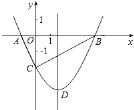
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A,B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A,B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当MC+MA的值最小时,求点M的坐标.
【答案】(1)抛物线的解析式为y=![]() x﹣2,顶点D的坐标为 (
x﹣2,顶点D的坐标为 (![]() ,﹣
,﹣![]() );(2)△ABC是直角三角形,证明见解析;(3)点M的坐标为(
);(2)△ABC是直角三角形,证明见解析;(3)点M的坐标为(![]() ,﹣
,﹣![]() ).
).
【解析】
(1)因为点A在抛物线上,所以将点A代入函数解析式即可求得答案;
(2)由函数解析式可以求得其与x轴、y轴的交点坐标,即可求得AB、BC、AC的长,由勾股定理的逆定理可得三角形的形状;
(3)根据抛物线的性质可得点A与点B关于对称轴x![]() 对称,求出点B,C的坐标,根据轴对称性,可得MA=MB,两点之间线段最短可知,MC+MB的值最小.则BC与直线x
对称,求出点B,C的坐标,根据轴对称性,可得MA=MB,两点之间线段最短可知,MC+MB的值最小.则BC与直线x![]() 交点即为M点,利用得到系数法求出直线BC的解析式,即可得到点M的坐标.
交点即为M点,利用得到系数法求出直线BC的解析式,即可得到点M的坐标.
(1)∵点A(﹣1,0)在抛物线y![]() bx﹣2上,∴
bx﹣2上,∴![]() b×(﹣1)﹣2=0,解得:b
b×(﹣1)﹣2=0,解得:b![]() ,∴抛物线的解析式为y
,∴抛物线的解析式为y![]() x﹣2.
x﹣2.
y![]() x﹣2
x﹣2![]() (x2﹣3x﹣4 )
(x2﹣3x﹣4 )![]() ,∴顶点D的坐标为 (
,∴顶点D的坐标为 (![]() ).
).
(2)当x=0时y=﹣2,∴C(0,﹣2),OC=2.
当y=0时,![]() x﹣2=0,∴x1=﹣1,x2=4,∴B (4,0),∴OA=1,OB=4,AB=5.
x﹣2=0,∴x1=﹣1,x2=4,∴B (4,0),∴OA=1,OB=4,AB=5.
∵AB2=25,AC2=OA2+OC2=5,BC2=OC2+OB2=20,∴AC2+BC2=AB2.∴△ABC是直角三角形.
(3)∵顶点D的坐标为 (![]() ),∴抛物线的对称轴为x
),∴抛物线的对称轴为x![]() .
.
∵抛物线y![]() x2+bx﹣2与x轴交于A,B两点,∴点A与点B关于对称轴x
x2+bx﹣2与x轴交于A,B两点,∴点A与点B关于对称轴x![]() 对称.
对称.
∵A(﹣1,0),∴点B的坐标为(4,0),当x=0时,y![]() x﹣2=﹣2,则点C的坐标为(0,﹣2),则BC与直线x
x﹣2=﹣2,则点C的坐标为(0,﹣2),则BC与直线x![]() 交点即为M点,如图,根据轴对称性,可得:MA=MB,两点之间线段最短可知,MC+MB的值最小.
交点即为M点,如图,根据轴对称性,可得:MA=MB,两点之间线段最短可知,MC+MB的值最小.
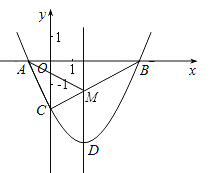
设直线BC的解析式为y=kx+b,把C(0,﹣2),B(4,0)代入,可得:![]() ,解得:
,解得: ,∴y
,∴y![]() x﹣2.
x﹣2.
当x![]() 时,y
时,y![]() ,∴点M的坐标为(
,∴点M的坐标为(![]() ).
).


科目:初中数学 来源: 题型:
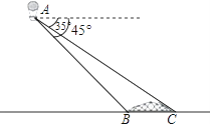
【题目】小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,求热气球离地面的高度.(结果保留整数)(参考数据:sin35°=0.57,cos35°=0.82,tan35°=0.70)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数,试问:按这种方法能组成哪些位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台“中国梦”栏目的一位记者乘汽车赴360km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路.若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是_____(填序号).
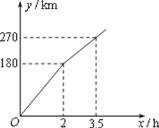
(1)汽车在高速公路上的行驶速度为100km/h
(2)乡村公路总长为90km
(3)汽车在乡村公路上的行驶速度为60km/h
(4)该记者在出发后5h到达采访地.
查看答案和解析>>
科目:初中数学 来源: 题型:
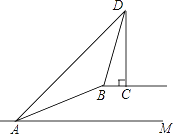
【题目】如图,斜坡AB的坡度为1:2.4,长度为26m,在坡顶B所在的平台上有一座电视塔CD,已知在A处测得塔顶D的仰角为45°,在B处测得塔顶D的仰角为73°,求电视塔CD的高度. (参考数值:sin73°≈ ![]() ,cos73°≈0.
,cos73°≈0. ![]() ,tan73°≈
,tan73°≈ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数y=4x﹣![]() x2刻画,斜坡可以用一次函数y=
x2刻画,斜坡可以用一次函数y=![]() x刻画,下列结论错误的是( )
x刻画,下列结论错误的是( )

A. 当小球抛出高度达到7.5m时,小球水平距O点水平距离为3m
B. 小球距O点水平距离超过4米呈下降趋势
C. 小球落地点距O点水平距离为7米
D. 斜坡的坡度为1:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习苏科版九下《锐角三角函数》一章时,小明同学对一个角的倍角的三角函数值是否具有关系产生了浓厚的兴趣,进行了一些研究.
(1)初步尝试:我们知道:tan60°= ,tan30°= ,发现结论:tanA 2tan![]() ∠A(填“=”或“≠”);
∠A(填“=”或“≠”);
(2)实践探究:如图1,在Rt△ABC中,∠C=90°,AC=2,BC=1,求tan![]() ∠A的值;小明想构造包含
∠A的值;小明想构造包含![]() ∠A的直角三角形:延长CA至D,使得DA=AB,连接BD,所以得到∠D=
∠A的直角三角形:延长CA至D,使得DA=AB,连接BD,所以得到∠D=![]() ∠A,即转化为求∠D的正切值.
∠A,即转化为求∠D的正切值.
请按小明的思路进行余下的求解:
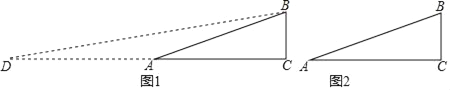
(3)拓展延伸:如图2,在Rt△ABC中,∠C=90°,AC=3,tanA=![]() .
.
①tan2A= ;
②求tan3A的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P、Q两点同时停止运动.设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系的图象是【 】

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com