
��ֲ��ݮ���Ż�����22�ֲ�ݮ���ۣ�������������������һ������ʡ��ֱ�������������̣������ڱ����г�����.���������������������������ÿ��������ÿ������������±���
| �������� | ÿ���������֣� | ÿ����������Ԫ�� |
| ʡ������ | �� | 1200 |
| �������� | �� | 2000 |
(1) y=��800x+44000��(2) 16��x��22��(3) ʡ������16�֣���������6��ʱ������������������31200Ԫ��
���������������1����������Ĺ�ϵ���ɵú�������ʽ��
��2����������ʱ��Ĺ�ϵ���ɵò���ʽ�飬���ݽⲻ��ʽ�飬�ɵô𰸣�
��3������һ�κ��������ʣ��ɵô𰸣�
�����������1����������ʽΪy=1200x+��22��x����2000��
��y=��800x+44000��
��2��������ʱ�䣬�� ��
��
���16��x��22��
��3��y=��800x+44000��
k=��800��0��y��x�����������
��x=16ʱ��y���=��800��16+44000=31200��
��ʡ������16�֣���������6��ʱ������������������31200Ԫ��
���㣺һ�κ�����Ӧ�ã�


 ��ѧ����ϵ�д�
��ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪��P��a��b����һ�κ���y=4x+3��ͼ���ϣ������ʽ4a��b��2��ֵ������ ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��һ�����������У�һ��������һ������Ӽ������ҵأ������ҵ�ж���أ��������Ӽس���x��h��ʱ��������صľ���Ϊy��km����y��x�ĺ�����ϵ��ͼ��ʾ������ͼ����Ϣ�ش��������⣺
��1���������صľ����� ��
��2�������ҵغ�ж���õ�ʱ���� ��
��3�������������ص��ٶ��� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ƽ��ֱ������ϵϵxOy�У�ֱ��y=2x+m��y�ύ�ڵ�A����ֱ��y=��x+4���ڵ�B��3��n����PΪֱ��y=��x+4��һ�㣮
��1����m��n��ֵ��
��2�����߶�AP���ʱ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪����ƽ��ֱ������ϵ�У���A��B�ֱ���x���������ϣ����߶�OA��OB��OA��OB���ij��ֱ���ڷ���x2��5x+4=0������������C��y���������ϣ���OB=2OC��
��1����ȷ��ֱ��BC�Ľ���ʽ��
��2�������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ֱ��y= ��x�ᣬy��ֱ��ڵ�E��F����A���߶�EF��һ���㣨�����E�غϣ�������A��x�ᴹ�ߣ������ǵ�B����ABΪ������������ABCD��AB��BC=3��4��
��x�ᣬy��ֱ��ڵ�E��F����A���߶�EF��һ���㣨�����E�غϣ�������A��x�ᴹ�ߣ������ǵ�B����ABΪ������������ABCD��AB��BC=3��4��
��1������A���F�غ�ʱ����֤���ı���ADBE��ƽ���ı��Σ�����ֱ��DE�ı���ʽ��
��2������A�����F�غ�ʱ���ı���ADBE��Ȼ��ƽ���ı��Σ�˵�����ɣ���ʱ�㻹�����ֱ��DE�ı���ʽ�����ܣ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����A��1��6���͵�M��m��n�����ڷ���������y= ��x��0����ͼ���ϣ�
��x��0����ͼ���ϣ�
��1��k��ֵΪ�� ����
��2����m=3����ֱ��AM�Ľ���ʽ��
��3����m��1ʱ������M��MP��x�ᣬ����ΪP������A��AB��y�ᣬ����ΪB�����ж�ֱ��BP��ֱ��AM��λ�ù�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�������
��ֱ֪�� ��
�� �ύ�ڵ�A(��4��0)����
�ύ�ڵ�A(��4��0)���� �ύ�ڵ�B.
�ύ�ڵ�B.
��С��1����b��ֵ
��С��2���ѡ�AOB��ԭ��O˳ʱ����ת90���A���� ���
��� ������B����
������B���� ���
��� ����
����
����ֱ�� �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
����ֱ��AB��ֱ�� ���ڵ�C������PQMN�ǡ�
���ڵ�C������PQMN�ǡ� ���ڽӾ��Σ����е�P��Q���߶�
���ڽӾ��Σ����е�P��Q���߶�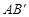 �ϣ���M���߶�
�ϣ���M���߶� �ϣ���N���߶�AC��.������PQMN�������ڱߵı�Ϊ1��2���������PQMN���ܳ�.
�ϣ���N���߶�AC��.������PQMN�������ڱߵı�Ϊ1��2���������PQMN���ܳ�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com